Оценивание законов распределения случайных величин (Раздел 4 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 5

По определению функция распределения  случайной величины  есть вероятность случайного события:

                                                 .

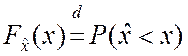Пусть в качестве её оценки  используется частота статистического аналога x_i < x события  < x в серии n испытаний:

                                       .         (4.3.4)

Поскольку (4.3.4) является оценкой вероятности случайного события  < x, то её качество должно исследоваться методами, рассмотренными в § 3.3.

Если объём выборки достаточно велик, то закон распределения оценки функции  может быть аппроксимирован нормальным законом аналогично (3.3.4):

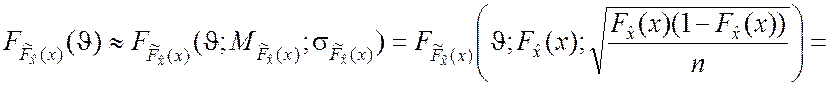
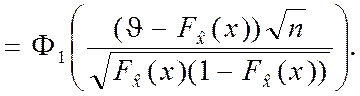                                                               (4.3.5)

С учётом (4.3.5) по аналогии с формулами (3.3.5) – (3.3.7) получим

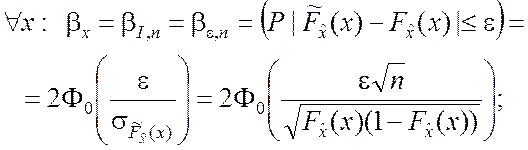                                (4.3.6)

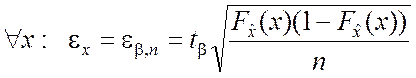                                ;   (4.3.7)

               .                                                         (4.3.8)

При исследовании качества оценки  возникает проблема, связанная с незнанием истинной функции распределения . При большом объёме выборки эта функция заменяется её оценкой  и формулы (4.3.6) – (4.3.8) приобретают вид:

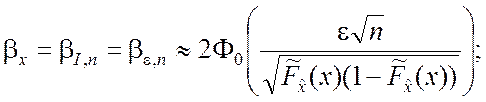                                                                                     (4.3.9)

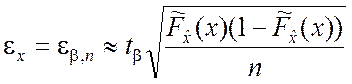                                     ;      (4.3.10)

                                   .    (4.3.11)

Из соотношений (4.3.6) – (4.3.11) видно, что все показатели качества оценивания функции распределения  зависят от её аргумента x. Так, при фиксированных доверительной вероятности b = const и объёме выборки n = const доверительные границы для  будут функциями:

                                        .                  

П р и м е р 4.4. Пусть признак  массива экспериментальных данных распределён нормально, т.е.

                          .

По результатам ста наблюдений (n = 100) построена статистическая функция распределения

                                        .

Требуется построить для функции распределения 95-процентный доверительный интервал (b = 0,95).

▼ По формулам (4.3.7) и (4.3.8) получим

               ;                                                              

.                                                             

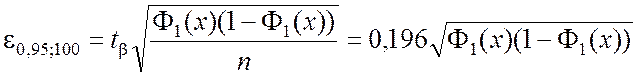На рис.4.6 изображена доверительная область для функции , границы которой даны пунктиром. График функции  – сплошная линия.                                                                                              ▲

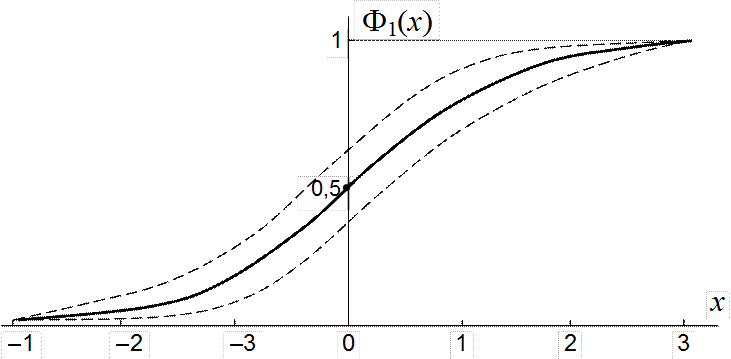
Рис.4.6. Доверительная область функции распределения (к примеру 4.4)

4.3.5. Потребный объём экспериментальных данных

Поскольку  является оценкой вероятности случайного события  < x, то объём n выборки, потребный для оценивания функции распределения  с необходимыми точностью e и надёжностью b, определяется выражением, аналогичным (3.3.8):

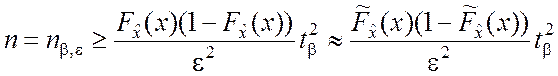                      .                                                        (4.3.12)

Как видно из рис.4.6, доверительная область для  зависит от x и имеет наибольшую ширину при . Это означает, что наибольшее число наблюдений потребуется для оценивания значения  (см. табл.3.1). Согласно формуле (4.3.12) и табл.3.1. при x ® ¥ потребное число n экспериментальных точек снижается, однако при этом уменьшается правомерность предположения о нормальном распределении оценки . Поэтому при оценивании функции распределения объём выборки берётся максимальным, обеспечивающим требуемые точность и надёжность оценки  при всех x Î {x}. Указанный объём определяется соотношением

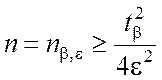                                                   .                   (4.3.13)