Программы линейной структуры. Простейшие программы циклической структуры. Разветвления, циклы и разветвления. Простейшие алгоритмы обработки массивов, страница 6

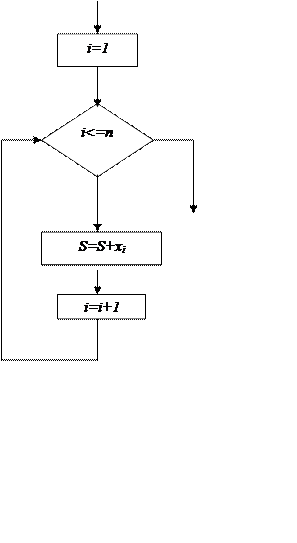
В приведенных типовых алгоритмах циклы органи­зуются при помощи управляющей переменной цикла  for. Для таких циклов может быть предложена более деталь­ная структура (рис. 1), в которой выделены блоки, организующие цикл; задание начального значения (I_нач) управляющей переменной цикла (I), изменение управляющей переменной цикла на шаг (Н) и проверка достижения конечного значения (I_КОн) управляющей переменной цикла. Управляющую переменную цикла называют счет­чиком, а организуемый при помощи нее цикл — циклом по счетчику. В блоке «Начальные присваивания» должны задаваться значения переменных, используемых в теле цикла (или в блоке проверки ус­ловия), из тех соображений, чтобы при первом прохождении цикла получался правильный результат. Например, при вычислении суммы n слагаемых после первого прохождения цикла сумма S                                                       

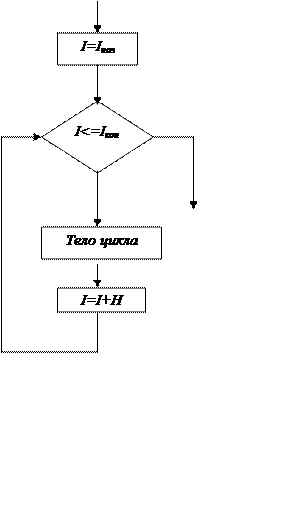
                                                            Рис. 1                                        Рис. 2

                                                                                                                              

                                                                                                                            

                                                                         нет                                                                            нет

                                                   да                                                                               да

должна быть равна первому слагаемому, т. е. после первого выпол­нения оператора S=S+x_i (при i=1) должно быть S=x₁а для этого в блоке «Начальные присваивания» нужно задать S=0 (см. рис. 2). Аналогично, при вычислении произведения п сомножи­телей (п. 2) после первого выполнения оператора Р=Р* х_i (при i=l) должно быть P= х₁ , а для этого в блоке «Начальные присваивания» нужно задать Р=1 (см. рис. 3) и т. д.

                                                                                                   n

1.  Вычисление суммы п слагаемых. Требуется вычислить S= Sx_i , где x_i– i-й член суммы, зависящий от i.

i=1 

Например, при x_i=iSравно  сумме   первых  п  натуральных   чисел.  Задача сводится к организации цикла по i. При каждом прохождении цикла значение S увеличивается на очередной член сум­мы. До входа в цикл нужно задать S=0 (рис. 2).

Программа 2.1 реализует приведенный алгоритм для вычисления суммы первых 15 натуральных чисел (x_i=i,S =15).

Программа 2.1

void main()

{

  int S=0, i;

   for (i=1; i<=15; i=i +1 )

    S=S+i;

printf( “Сумма первых 15 натуральных чисел равна: %i ”, S);

}

В некоторых случаях для уменьшения общего количества вы­полняемых арифметических операций целесообразно последующий член суммы вычислять, используя предыдущий. При этом для обозначения члена суммы нужно использовать вспомогательную переменную. Например, при вычислении

n

S= Sxⁱцелесообразно обозначить  с=хⁱи

i=1

для вычисления следующего члена домножить предыдущий на х (с=с*х).

В некоторых случаях, например, при  x_i =(—1)ⁱ * i²  такой прием целесообразно приме­нять к одному из сомножителей члена суммы, а именно вычислять с=(-1)ⁱдля следую­щего члена суммы как с=—с. До входа в цикл (для первого члена) нужно положить с= 1.

В качестве примера, иллюстрирующего рассмотренный прием, составим программу для вычисления следующей суммы  

     10

S= S(—1)ⁱ(1+p)²ⁱ/i.

     i=1

  при  заданном   значении р=3,5.

Член суммы представим как с/i, где с= =(—1)ⁱ(1+р)²ⁱ.  Для каждого следующего чле­на суммы с будем вычислять по рекуррентной формуле с= - с(1+p)², где в правой части используется значение с для предыдущего члена. До входа в цикл положим с=1  и с для пер­вого члена суммы будем вычислять по общей формуле (програм­ма 2.2).

Программа 2.2

void  main()

{

float p=3.5, c=1, s=0;