|
|
Рис.5.3 |
Модель поляризованного диэлектрика для расчета микроскопического поля, поляризующего молекулу. Поле внутри полости создается “хвостами” молекул ближайшего окружения. |
|
|
(5.29) |
Микроскопическое поле внутри полости в диэлектрике, окружающей молекулу. |
|
|
(5.30) |
Уравнение для вектора поляризации в случае плотного диэлектрика. |
|
|
(5.31) |
Решение уравнения (30), “предсказывающее” возможность существования сегнетоэлектриков. |
|
|
(5.32) |
Одна из возможных форм записи формулы Клаузиуса - Массотти. |
Задачи для самостоятельного решения
5.1. Доказать теорему (5.4) в дифференциальной формулировке, не используя ее интегральный аналог (5.6). Указание: применить закон сохранения заряда для бесконечно малого объема поляризующегося вещества.
5.2. Найти электрическое поле, создаваемое бесконечным цилиндром, однородно поляризованном в направлении, перпендикулярном его оси.
5.3. Длинный прямой кабель представляет собой металлический провод, помещенный на ось металлической трубки - оплетки. Внутренний провод отделен от оплетки слоем диэлектрика, проницаемость которого изменяется в перпендикулярном оси направлении по известному закону: e=e(r). Определить электрическое поле в произвольной точке пространства, если провод несет постоянный линейный заряд l, а полный заряд оплетки равен нулю. Указание: воспользоваться теоремой о потоке вектора электрической индукции.
5.4. Диэлектрическую пластинку, поперечные размеры которой много больше толщины, внесли в однородное электростатическое поле, расположив перпендикулярно силовым линиям. Определить напряженность поля в произвольной точке пространства и распределение поляризационных зарядов в пластинке, если ее диэлектрическая проницаемость изменяется по толщине в соответствии с заданным законом e=f(h).
5.5. В рассмотренном примере о заряде над полупространством из диэлектрика использовалось только граничное условие для вектора D. Какую информацию в этом случае несет граничное условие для Е?
5.6. Найти электростатическое поле, создаваемое системой из заряда, помещенного в однородный изотропный диэлектрик, заполняющий полупространство с плоской границей.
5.7. Определить силу взаимодействия электрического диполя с полупространством из однородного изотропного диэлектрика с известным e. Дипольный момент ориентирован перпендикулярно плоской границе диэлектрика. Расстояние от диполя до границы известно.
5.8. В однородное поле напряженностью E0 внесли шар из однородного изотропного диэлектрика с проницаемостью e. Радиус шара известен - R. Определить напряженность электрического поля в произвольной точке пространства. Указание: попытайтесь доказать, что однородный диэлектрический шар в однородном поле поляризуется однородно. Использование этого свойства существенно облегчает решение задачи.
5.9. Решите задачу 5.6 для случая однородного бесконечного цилиндра, ось которого перпендикулярна исходному полю. Изобразите примерную картину линий для векторов E и D.
5.10 Известно, что вектор напряженности электрического поля в анизотропном диэлектрике составляет угол a с осью z, а его величина равна Е. Определить модули векторов поляризации и электрической индукции, если тензор диэлектрической проницаемости дается матрицей вида:
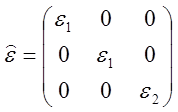 .
.
|
Соотношения, которые полезно помнить |
|
|
|
Вектор поляризации. |
|
|
Вектор электрической индукции. |
|
|
Уравнения для электростатического поля при наличии диэлектриков. |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.