Из за
большого различия масс ионов и электронов, влияние движения тяжелых частиц (ионов) на быстрый (высокочастотный)
процесс оказывается слабым, если ![]() . Ниже будет показано,
что при
. Ниже будет показано,
что при ![]() влияние ионов становится существенным.
влияние ионов становится существенным.
13.5. Диффузия плазмы. Рассмотрим достаточно медленный процесс при наличии частых столкновений электронов с тяжелыми частицами (ионами и нейтральными частицами):
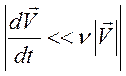
и пренебрежем инерционным членом в уравнении движения электронной компоненты
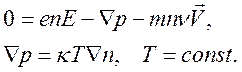
Получаем соотношение
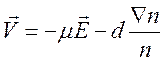 ,
,
или
,
где
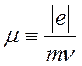 - подвижность,
- подвижность, 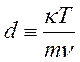 -
коэффициент диффузии,
-
коэффициент диффузии, ![]() - поток электронной компоненты
плазмы. Имеет место соотношение Эйнштейна
- поток электронной компоненты
плазмы. Имеет место соотношение Эйнштейна
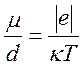 .
.
В
случае выполнения неравенства ![]() имеет место
диффузионный процесс. Он описывается законом Фика
имеет место
диффузионный процесс. Он описывается законом Фика
![]() .
.
В
этом приближении существует поток электронов из области большей их концентрации
в область меньшей концентрации. Если неравенство ![]() нарушается,
то ситуация усложняется за счет влияния электромагнитного взаимодействия
заряженных компонент. Уравнение неразрывности принимает вид
нарушается,
то ситуация усложняется за счет влияния электромагнитного взаимодействия
заряженных компонент. Уравнение неразрывности принимает вид
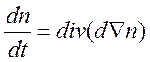 .
.
В случае полей малой амплитуды (в линейном приближении) последнее уравнение упрощается
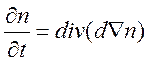 .
.
13.6.
Диффузия в слое плазмы, ограниченном стенками. Рассмотрим эволюцию одномерного пространственного
распределения плазмы между двумя стенками в случае ![]() . Будем
считать, что на стенках
. Будем
считать, что на стенках ![]() концентрация обращается
в ноль. Уравнение диффузии имеет вид
концентрация обращается
в ноль. Уравнение диффузии имеет вид
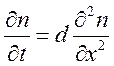 .
.
С такими граничными условиями это уравнение имеет бесконечно много решений. Одно из них (наинизшая мода, или нулевая мода) представляется в виде произведения двух функций
![]() .
.
Уравнению диффузии можно придать вид
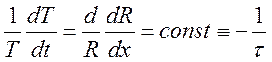 .
.
Получаем следующее представление
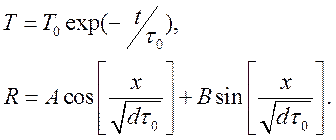
Для
решения с одним максимумом, из граничных условий получаем значения двух
констант 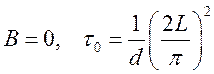 . Это соответствует описанию наинизшей
(нулевой) моде:
. Это соответствует описанию наинизшей
(нулевой) моде:
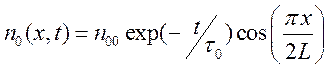 ,
, 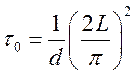 .
.
Если
известно начальное распределение концентрации ![]() ,
, ![]() , то можно построить решение нестационарной
задачи методом разделения переменных. Сделаем разложение в ряд Фурье:
, то можно построить решение нестационарной
задачи методом разделения переменных. Сделаем разложение в ряд Фурье:
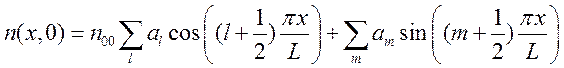 .
.
Правая
часть этого представления обращается в ноль при ![]() .
Решение нестационарной задачи можно построить в виде
.
Решение нестационарной задачи можно построить в виде
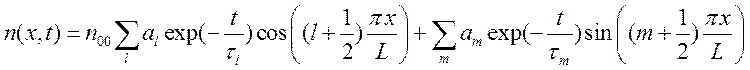 .
.
Подстановка
этого представления в уравнение диффузии и приравнивание коэффициентов при ![]() и
и ![]() дает
представление для масштаба затухания
дает
представление для масштаба затухания ![]() -й моды
-й моды
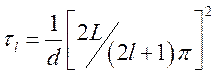 .
.
Гармоники
с большими номерами затухают быстрее, чем гармоники с меньшими номерами.
Постепенно начальное распределение ![]() превратится в нулевую
моду. Потом будет происходить уменьшение амплитуды, в то время, как форма
распределения будет оставаться неизменной.
превратится в нулевую
моду. Потом будет происходить уменьшение амплитуды, в то время, как форма
распределения будет оставаться неизменной.
13.7.
Действие статического источника ионизации в плазменном слое. В экспериментальных установках возможно поддержание
установившегося стационарного состояния путем непрерывной дополнительной
ионизации или инжекции плазмы. При этом компенсируются потери за счет диффузии.
Рассмотрение такой ситуации возможно при добавлении в уравнение дополнительного
члена ![]() , описывающего источник:
, описывающего источник:
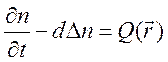 .
.
В
установившемся состоянии 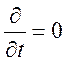 и возникает задача о
решении уравнения Пуассона со сторонним источником. Рассмотрим ситуацию когда
и возникает задача о
решении уравнения Пуассона со сторонним источником. Рассмотрим ситуацию когда ![]() .
.
Если
источник локализован в плоскости и он действует в слое ![]() ,
то при
,
то при ![]() имеем уравнение
имеем уравнение 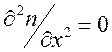 .
Граничные условия возьмем в виде
.
Граничные условия возьмем в виде ![]() . Решение такой задачи
имеет представление
. Решение такой задачи
имеет представление
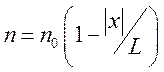 .
.
В
точке расположения ![]() - образного источника происходит
скачок производной.
- образного источника происходит
скачок производной.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.