Основные понятия физики плазмы. Электродинамика быстрых процессов в плазме, страница 6

                                                .

Поэтому групповая скорость равна нулю

                                                .

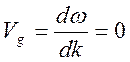Описанное плазменное колебание – это предельный случай волнового процесса при .

            Рассмотрим уравнение Кулона в виде

                                                ,

которое для фурье – образа дает , последнее справедливо, так как для продольной волны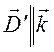. Следовательно, ,  . Значит, для продольных полей имеет место свойство

                                                .

Этим свойством обладают не только продольные колебания, но и волновые продольные поля в изотропной плазме.

            2). Продольные плазменные волны в горячей плазме. Пренебрежение хаотическим тепловым движением электронов (), как показано выше, приводит к тому, что в изотропной плазме линейный продольный волновой процесс вырождается в колебательный. Выясним влияние конечности температуры на продольный волновой процесс. Используем линеаризованные уравнения движения и неразрывности

                                               

                                                .

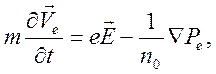
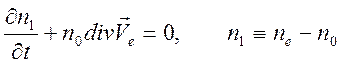В таком приближении не учитывается сила трения за счет упругих соударений электронов с ионами и нейтральными частицами. Так как процесс продольный, то  и для описания электрического поля достаточно использовать уравнение Кулона

                                                .

Система этих трех уравнений не замкнута, необходимо добавить уравнение, описывающее давление  (уравнение состояния для давления). Ограничимся здесь простейшим уравнением состояния совершенного газа

                                    .

Множитель 3 в формуле для  учитывает упорядоченность движения электронов в возмущениях плазмы. Более строго учет этого множителя доказывается в кинетической теории плазмы. Пренебрегая возмущениями температуры, линеаризованное уравнение состояния получим в виде

.

Получим дисперсионное уравнение. Это можно сделать, например, исключив из системы : Уравнение для фурье - образа  имеет вид

                                    .

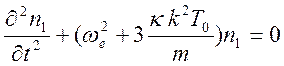Дисперсионное уравнение приводится к форме

                                                ,

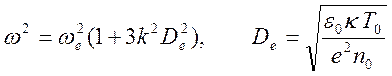либо

                                                .

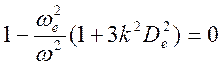Последняя формула дает представление для  в случае продольных волн:

                                                ..

Учет влияния конечности температуры электронной компоненты приводит к наличию пространственной дисперсии у продольного процесса. Признаком этого является зависимость  от . В отличие от ситуации, анализированной в пункте1) данного раздела, возникает связь  и фазовая скорость описывается соотношением

                                               

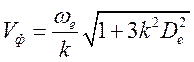
Групповая скорость отлична от нуля (колебательный процесс превращается в волновой)

                                                .

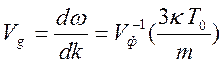Для продольной волны справедливо свойство 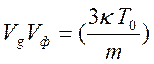. Напомним, что для волны поперечной было:  и конечность температуры электронной компоненты не влияла на дисперсионные свойства плазмы.

Переход к приближению холодной плазмы осуществляется при выполнении условия

                                                 или .

Это случай длинноволнового приближения.

            Более точное кинетическое описание продольной волны дает дисперсионное уравнение при :

                                    .

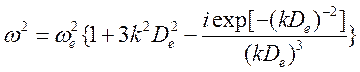Кинетическая теория подтверждает правильность сделанного выше допущения . Отметим, что кинетическое описание дает дисперсионное уравнение не в алгебраической форме. В такой более точной теории, даже без учета столкновений (бесстолкновительная плазма) функция  является комплексной. Это соответствует затуханию продольной волны. Такое затухание называется затуханием Ландау (1946 г.), оно обусловлено тем, что происходит резонансное взаимодействие частиц с полем продольной волны. Взаимодействие особо эффективно в том случае, когда фазовая скорость волны близка к проекции скорости частицы на направление волнового вектора. Медленные электроны (их гораздо больше, чем быстрых электронов) «отбирают» у электрической волны больше энергии, чем быстрые «отдают» ее волне. Под действием электрического поля распределение электронов по скоростям изменяется так, что оно отличается от максвелловского. Этого эффекта нет в приближении сплошной среды – это кинетическое явление.