Частицы
плазмы находятся в состоянии хаотического теплового движения. Для
характеристики этого движения вводится понятие температуры плазмы в
целом ![]() и отдельных ее компонент
и отдельных ее компонент ![]() . Температура плазмы
. Температура плазмы ![]() вводится в том случае, если плазма в целом
находится в состоянии термодинамического равновесия. При этом функции
распределения частиц всех сортов по импульсам являются максвелловскими с одной
и той же температурой
вводится в том случае, если плазма в целом
находится в состоянии термодинамического равновесия. При этом функции
распределения частиц всех сортов по импульсам являются максвелловскими с одной
и той же температурой ![]() . Такая плазма называется изотермической.
Часто в плазме имеется неизотермическое состояние, когда отдельные
ее компоненты имеют максвелловские распределения по импульсам с различными
температурами
. Такая плазма называется изотермической.
Часто в плазме имеется неизотермическое состояние, когда отдельные
ее компоненты имеют максвелловские распределения по импульсам с различными
температурами ![]() . Температура
. Температура ![]() характеризует среднюю кинетическую энергию
теплового движения частиц данного сорта
характеризует среднюю кинетическую энергию
теплового движения частиц данного сорта
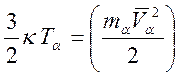 ,
,
где
![]() - постоянная Больцмана,
- постоянная Больцмана, ![]() - скорость хаотического теплового движения
частиц сорта
- скорость хаотического теплового движения
частиц сорта ![]() .
.
Сделаем несколько замечаний о вырожденной плазме, которая может существовать в области низких температур. Вырождение возможно для частиц с полуцелым спином (электроны, дырки, атомы водорода), когда тепловая энергия меньше энергии Ферми:
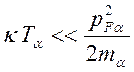 ,
,
где
![]() - граничный импульс Ферми. При этом
равновесное распределение частиц по импульсам определяется функцией
распределения Ферми. В вырожденной плазме понятие температуры, как меры энергии
среднего хаотического движения теряет смысл. Эту роль играет энергия Ферми
- граничный импульс Ферми. При этом
равновесное распределение частиц по импульсам определяется функцией
распределения Ферми. В вырожденной плазме понятие температуры, как меры энергии
среднего хаотического движения теряет смысл. Эту роль играет энергия Ферми 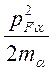 , не зависящая от температуры плазмы и
возрастающая с увеличением концентрации частиц. В металлах концентрация
свободных носителей заряда порядка
, не зависящая от температуры плазмы и
возрастающая с увеличением концентрации частиц. В металлах концентрация
свободных носителей заряда порядка ![]() . При столь высоких
концентрациях свободные электроны оказываются вырожденными при
. При столь высоких
концентрациях свободные электроны оказываются вырожденными при ![]() . Твердотельная плазма может быть как вырожденной,
так и не вырожденной.
. Твердотельная плазма может быть как вырожденной,
так и не вырожденной.
3). Предварительное определение понятий: квазинейтральность, плазменная частота, дебаевский радиус. Не всякий ионизованный газ представляет содой плазму. Нужно еще, чтобы он обладал свойством квазинейтральности. В среднем за достаточно большой промежуток времени и в достаточно больших объемах газ должен быть в целом нейтральным. Выясним, каковы характерные временные и пространственные масштабы разделения зарядов и нарушения нейтральности плазмы. Требование нейтральности накладывает ограничение на величины концентраций электронов и ионов:
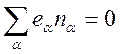 .
.
В
случае, когда в плазме имеются только однократно ионизированные ионы одного
сорта, это условие записывается в виде ![]() .
.
Из простых физических соображений оценим временной масштаб разделения зарядов. Представим себе, что электрон плазмы отклонился на расстояние порядка величины среднего расстояния между частицами
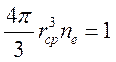 , или
, или 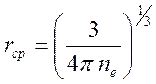 .
.
При этом возникает кулоновская возвращающая сила, по порядку величины равная силе взаимодействия двух электронов
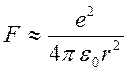 .
.
Уравнение
движения электрона 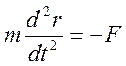 сведется к соотношению для
частоты колебаний электрона
сведется к соотношению для
частоты колебаний электрона 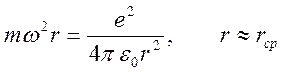 . В результате, имеем
. В результате, имеем
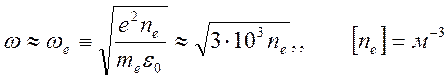 .
.
Частота
![]() называется электронной ленгмюровской,
электронной плазменной или просто плазменной частотой. За временной
масштаб разделения зарядов можно принять величину
называется электронной ленгмюровской,
электронной плазменной или просто плазменной частотой. За временной
масштаб разделения зарядов можно принять величину
![]() .
.
Для
ионосферной плазмы ![]() для термоядерной плазмы и плазмы
газового разряда
для термоядерной плазмы и плазмы
газового разряда ![]() для плазмы твердых тел
для плазмы твердых тел ![]()
Пространственный
масштаб разделения зарядов ![]() можно оценить, исходя
из того, что его величина определяется расстоянием на которое может сместиться
возмущение плотности заряженных частиц вследствие их теплового движения со
скоростью
можно оценить, исходя
из того, что его величина определяется расстоянием на которое может сместиться
возмущение плотности заряженных частиц вследствие их теплового движения со
скоростью ![]() за время, равное периоду плазменных
колебаний
за время, равное периоду плазменных
колебаний
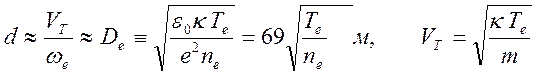 . (13.1)
. (13.1)
Здесь
![]() носит название электронного дебаевского
радиуса. Для вырожденной плазмы энергия хаотического движения электронов
представляет собой энергию Ферми, поэтому в формуле (13.1) нужно
носит название электронного дебаевского
радиуса. Для вырожденной плазмы энергия хаотического движения электронов
представляет собой энергию Ферми, поэтому в формуле (13.1) нужно ![]() заменить на
заменить на ![]() :
:
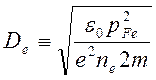 .
.
Для
квазинейтральности плазмы необходимо, чтобы ее характерные пространственные
масштабы ![]() были много больше дебаевского радиуса
были много больше дебаевского радиуса
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.