Основные понятия физики плазмы. Электродинамика быстрых процессов в плазме, страница 5

Пусть в начале координат закреплен точечный заряд , и он окружен плазмой. Будем рассматривать плазму как две взаимодействующие сплошные среды. Требуется найти установившееся статическое распределение потенциала поля. Потенциал удовлетворяет уравнению

                                                ,

где штрихом отмечены возмущенные значения полей,  - заряд электрона. Для статической ситуации уравнения движения электронной и ионной компонент имеют вид нелинейных уравнений

                                    .                         (13.3.А)

Для описания давления используем уравнение состояния совершенного газа

                                                .

Ниже ограничимся идеализацией . Так как в электростатике , то уравнения движения принимают вид

                                                .

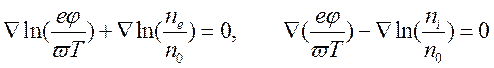Получаем нелинейные представления для концентраций

.

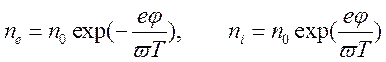Уравнение (13.3А) принимает вид неоднородного нелинейного уравнения

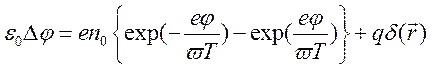                        .           (13.3.Б)

Построим решение , удовлетворяющее граничным условиям

.

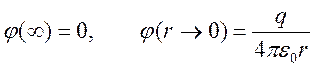Для описания процессов в плазме наибольший интерес представляет ситуация, когда потенциальная энергия взаимодействия заряженных частиц мала по сравнению с их кинетической энергией (это есть условие газового приближения):

                                                .

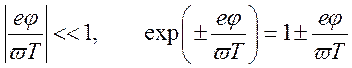В такой ситуации уравнение (13.3.Б) становится линейным однородным

                                                ,          

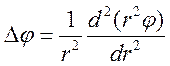
Где 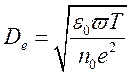 - введенный ранее радиус экранирования Дебая. Так как невозмущенное состояние однородно и заряд  - точечный, то будет иметь место сферическая симметрия

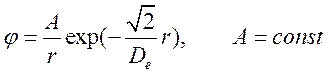                                                .Постоянную  выбираем из требования предельного перехода к кулоновскому полю при  (строго говоря, в полученном приближенном решении нельзя делать переход к случаю так как при этом нарушается неравенство ):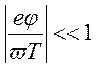

                                                .

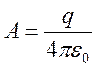Потенциал  в области  экспоненциально мал. Здесь поле заряда  экранировано полем зарядов противоположного знака. Это обеспечивает электронейтральность плазмы при . Электронейтральность нарушается в области .

Полученное таким образом приближенное решение пригодно на больших расстояниях, когда 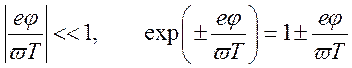 и это решение применимо в малой окрестности около заряженной частицы

13.4. Продольные плазменные колебания в холодной плазме. Продольные плазменные волны в горячей плазме.

            1). Продольные плазменные колебания в холодной плазме. В случае продольного процесса  рассмотрим быстропеременные поля, считая ионную компоненту неподвижной. Закон Кулона возьмем в виде

                                               

где  - невозмущенная концентрация электронной компоненты плазмы,  - возмущенное значение ее. В случае полей малой амплитуды , используем уравнение неразрывности и уравнение движения в линеаризованном виде (ограничимся сейчас приближением холодной плазмы: , без учета влияния столкновений )

                                                ,

                                                .

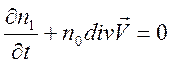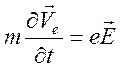Применяя операцию  к уравнению движения и учитывая закон Кулона, получим

                                                .

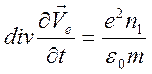Уравнение неразрывности совместно с последним уравнением позволяет получить

                                                .

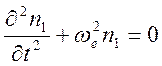Решение этого уравнения описывает гармонический процесс с плазменной частотой

                                                .

Решение имеет специфически вид произведения двух функций, каждая из которых зависит только от одного аргумента. Это не волновое, а колебательное явление (отсутствует процесс распространения), описанный Ленгмюром (1926 г.). Эти колебания называют плазменными, или ленгмюровскими. Иногда их называют электростатическими, так как электрическое поле потенциально: . Однако, на самом деле эти колебания не являются статическими, так как 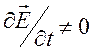. Для плоских монохроматических волн (фурье – образов полей) получается дисперсионное уравнение, в которое не входит волновое числопоэтому частота не зависит от волнового числа :