![]() .
.
Только
при этом условии можно систему заряженных частиц считать плазмой, т.е.
материальной средой с новыми качественными свойствами. В противном случае будет
простая совокупность отдельных заряженных частиц в вакууме. Для земной
ионосферы ![]() для термоядерной плазмы и плазмы газового
разряда
для термоядерной плазмы и плазмы газового
разряда ![]() для плазмы твердых тел
для плазмы твердых тел ![]()
4). Газовое приближение. Плазменный параметр. В приведенном выше определении плазма была охарактеризована, как газ заряженных частиц. Газом нельзя считать любую систему частиц. Совокупность частиц образует газ (применимо газовое приближение), если средняя потенциальная энергия частиц мала по сравнению с их средней кинетической (тепловой) энергией. Для кулоновски взаимодействующих частиц указанное условие записывается в виде
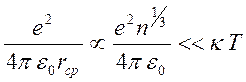 .
.
С этим неравенством связана важная безразмерная характеристика плазмы
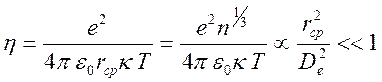 .
.
Величина
![]() называется плазменным параметром, и
условие применимости газового приближения сводится к требованию
называется плазменным параметром, и
условие применимости газового приближения сводится к требованию ![]() . Среднее расстояние между заряженными
частицами в плазме должно быть меньше дебаевского радиуса. Или иначе, внутри
дебаевской сферы (сфера с радиусом
. Среднее расстояние между заряженными
частицами в плазме должно быть меньше дебаевского радиуса. Или иначе, внутри
дебаевской сферы (сфера с радиусом ![]() ) должно находиться
много частиц:
) должно находиться
много частиц: 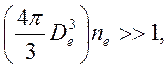 или
или 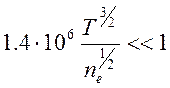 .
.
Для
вырожденной плазмы плазменный параметр ![]() есть
отношение средней потенциальной энергии к энергии Ферми
есть
отношение средней потенциальной энергии к энергии Ферми
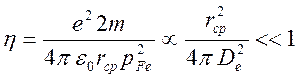 .
.
Газовое
приближение в металлах применимо лишь при концентрации носителей заряда ![]() . Для реальных металлов условие
. Для реальных металлов условие ![]() находится на грани применимости. В
полупроводниках эффективная масса носителей порядка величины
находится на грани применимости. В
полупроводниках эффективная масса носителей порядка величины ![]() и условие
и условие ![]() выполняется
при
выполняется
при ![]() .
.
13.2. Уравнения электродинамики быстропеременных процессов в плазме. Диэлектрическая проницаемость однородной изотропной плазмы.
1). Электромагнитные поля в плазме могут создаваться как внешними источниками, так и внутренним неоднородным и нестационарным распределением зарядов. В плазме возникает самосогласованное взаимодействие заряженных частиц и поля. Основой системы уравнений, описывающей процессы в плазме, являются уравнения Максвелла (сами по себе эти уравнения не замкнуты и они должны быть дополнены уравнениями динамики)
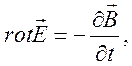
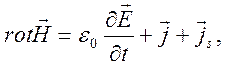
![]()
![]()
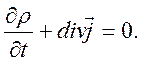
Эту систему необходимо дополнить уравнениями, описывающими материальные связи в плазме. В качестве таких дополнительных уравнений можно использовать уравнения динамики плазмы, как сплошной среды. Интересуясь сейчас свойствами быстропеременных полей в плазме, ограничимся следующим приближением. Ионы, как тяжелые частицы, будем считать неподвижными. Электронную компоненту опишем системой уравнений динамики (уравнений сплошной среды).
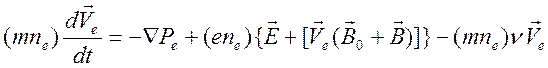 ,
,
это
уравнение движения. Здесь 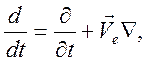
![]() - давление электронной компоненты,
- давление электронной компоненты, ![]() - частота упругих соударений электронов с
частицами других сортов (ионами и нейтральными частицами),
- частота упругих соударений электронов с
частицами других сортов (ионами и нейтральными частицами), ![]() - внешнее магнитное поле,
- внешнее магнитное поле, ![]() . Уравнение движения – это нелинейное
уравнение в частных производных.
. Уравнение движения – это нелинейное
уравнение в частных производных.
Простейшее уравнение состояния для давления, это уравнение состояния совершенного газа
![]() ,
,
где
![]() - постоянная Больцмана
- постоянная Больцмана
Концентрация ![]() и
скорость
и
скорость ![]() связаны уравнением неразрывности
связаны уравнением неразрывности
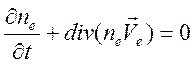 .
.
Ниже пренебрежем влиянием изменения температуры, и уравнение состояния для давления используем в виде
![]() .
. ![]() .
.
Здесь и ниже индексом нуль будем отмечать однородные невозмущенные значения полей. В невозмущенном состоянии электронную компоненту будем считать неподвижной и однородной. Интересуясь полями малой амплитуды, произведем линеаризацию:
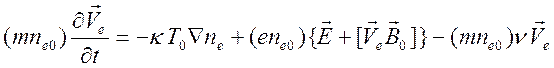 ,
,
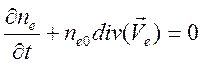 ,
,
где
![]() - частота столкновений электронов с ионами
и нейтральными частицами.
- частота столкновений электронов с ионами
и нейтральными частицами.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.