Основные понятия физики плазмы. Электродинамика быстрых процессов в плазме, страница 4

            2). Диэлектрическая проницаемость однородной изотропной плазмы. Пусть сторонние источники отсутствуют. Рассмотрим распространение плоских монохроматических поперечных волн в плазме, когда поля изменяются по закону

                                    .

При этом имеют место соотношения

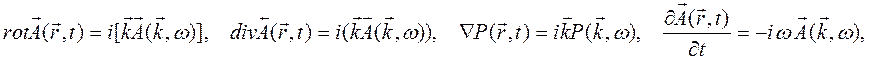
            где экспоненциальный множитель  опущен. Дифференциальные уравнения в частных производных с постоянными коэффициентами превратятся в алгебраические уравнения для комплексных амплитуд. Уравнения Максвелла примут вид

            ,            ,            .

Уравнение движения для поперечных волн принимает вид

                                    .

Следует подчеркнуть, что в уравнение движения для поперечных волн не входит сила газового давления, так как она параллельна вектору . В рассматриваемой здесь идеализации конечность температуры электронной компоненты не влияет на волновой процесс. Из уравнения непрерывности для поперечной волны следует, что  - не происходит возмущения концентрации электронов. Поэтому . Получили систему четырех однородных алгебраических уравнений для четырех комплексных амплитуд . Условие разрешимости системы – равенство нулю детерминанта (это характеристическое уравнение):

                                    ,        ,

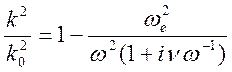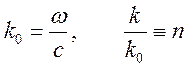где 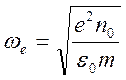 - электронная плазменная частота  - показатель преломления (не путать с концентрацией). Дисперсионное уравнение позволяет найти .

            Из системы уравнений

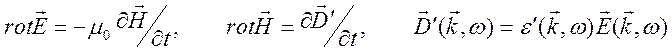
следует представление 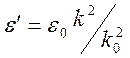. Поэтому из дисперсионного уравнения получается представление для показателя преломления  и для относительной комплексной диэлектрической проницаемости 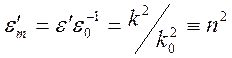. Таким образом, имеем

                                    .

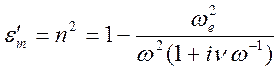Зависимость  от  - это признак наличия временной дисперсии, а зависимость  от волнового числа  - это признак наличия пространственной дисперсии. При  имеет место предельный переход к вакууму: . Волновой поперечный процесс в изотропной плазме не обладает пространственной дисперсией, так как 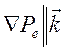. Воспользуемся соотношением

                                               

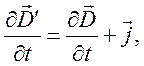
Имеющим Фурье – аналог

                                                .

Выражение для комплексной функции  представим в виде

                                

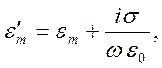
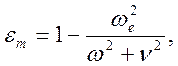
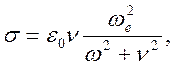
Рассмотрим два предельных случая

А). Пусть , тогда

                                                 

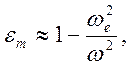
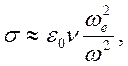
случай  соответствует отсутствию потерь, электропроводность  (в рассмотренном приближении единственный механизм диссипации это потеря энергии у электронной компоненты при упругих соударениях с ионами и нейтральными частицами). Если при  и плазменная частота удовлетворяет условию , то  обращается в нуль при  (Рис.13.1а). Если же ,  не обращается в нуль (Рис.13.1б), причем как в случае 11.1а и 11.1б имеет место универсальный предельный переход к вакууму: при.

Выясним основные дисперсионные закономерности при :

                                    ,

                        .

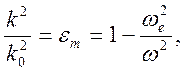
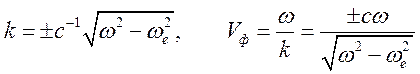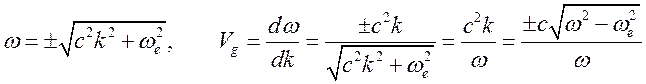Имеет место свойство:  при . На Рис. 13.2 показана зависимость фазовой (а) и групповой (б) скоростей от частоты. В области  скорости и  становятся чисто мнимыми (это область непрозрачности плазмы).

Б). Если  то получим приближенные формулы

                                     

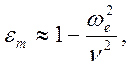
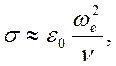
что соответствует отсутствию временной дисперсии. В рамках такого приближения нельзя переходить к пределу  при конечных значениях . Нельзя так же делать предельный переход , так как существует ограничение .

            Выясним условия применимости линеаризации

                                    ,

                                                .

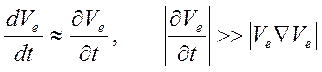Не трудно убедиться, что эти неравенства выполняются при условии

                                                .

13.3. Дебаевское экранирование. В следующем разделе понадобится понятие рарадиус Дебая. Оно уже обсуждалось раньше в разделе 13.1 на основе приближенных оценочныхисследований. Обсудим сейчас это понятие подробнее. Характерная длина, описывающая пространственный масштаб экранирования, впервые была введена Дебаем и Хюккелем (1923 г.) при рассмотрении процессов в сильных электролитах. В дальнейшем это понятие было перенесено в электродинамику плазмы. Рассмотрим идеализированную электростатическую ситуацию (строго говоря, это выходит за рамки данного раздела 13, так как в этом разделе рассматриваются быстропеременные процессы).