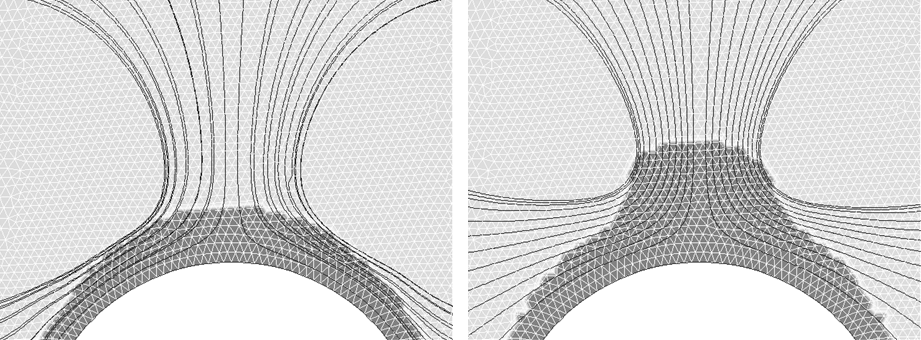
2. На втором шаге рассчитывается нестационарная гидродинамическая задача с распределенной нагрузкой в виде кулоновских сил, рассчитанных на первом шаге. Граничные условия: обе компоненты скорости на стенках равны нулю. Рассчитываются поля скоростей и давлений возникающих ЭГД-течений. После возникновения ЭГД-течений заряд из исходной овальной структуры выносится ЭГД-течением вдоль линий тока жидкости, формируя заряженную струю. Исходя из этих соображений, на втором шаге с помощью полученных распределений скоростей и линий тока жидкости рассчитывается новая область распределения объемного заряда. Для этого из полученного решения гидродинамической задачи строятся линии тока (рис.1a), проходящие через границу области первоначального распределения заряда, и рассчитывается смещение этой границы за некоторое время с учетом изменения скорости движения жидкости вдоль линий тока. Считается, что заряд перемещается вместе с жидкостью. Для достижения хорошей точности промежуток времени на следующую итерацию рассчитывается таким образом, чтобы граница зарядовой области сместилась не более чем на 0,5 толщины кольца. На рис.1b представлена область распределения плотности объемного заряда после четвертой итерации.
3. На третьем шаге решается электростатическая задача с новой областью распределения заряда, рассчитывается новое распределение электрических сил.
4. На четвертом шаге решается гидродинамическая задача с объемной нагрузкой, рассчитанной на третьем шаге. Строятся новые линии тока (рис.1b).
Далее итеративный процесс повторяется пока заряженная область не достигнет середины межэлектродного промежутка, где происходит встреча со струйкой, текущей от противоположного электрода. Затем рассматривается процесс распространиния заряженных струек вдоль оси симметрии с учетом рекомбинации, который рассматривается во второй части работы. Необходимо отметить, что разработанный алгоритм работает для данной модели автоматически, необходимо только вначале задать массивы определенного вида, описывающие начальную область распределения заряда. Далее программа сама переходит между задачами, рассчитывая смещение этой области вдоль линий тока. Ограничение на количество выполняемых итераций выставляется вручную.
Формирование ЭГД течения. В процессе распространения заряда вглубь межэлектродного промежутка изменяется область действия кулоновских сил (Рис.), действующих на жидкость, они как бы начинают сжимать заряженную область в тонкие струи толщиной порядка 1/3 диаметра электродов, по которым и распространяется в дальнейшем заряд, не растекаясь в стороны (в предположении, что заряд вморожен в жидкость). Процесс сужения струй с течением времени по мере распространения заряда представлен в виде динамики изменения линий тока (Рис.).
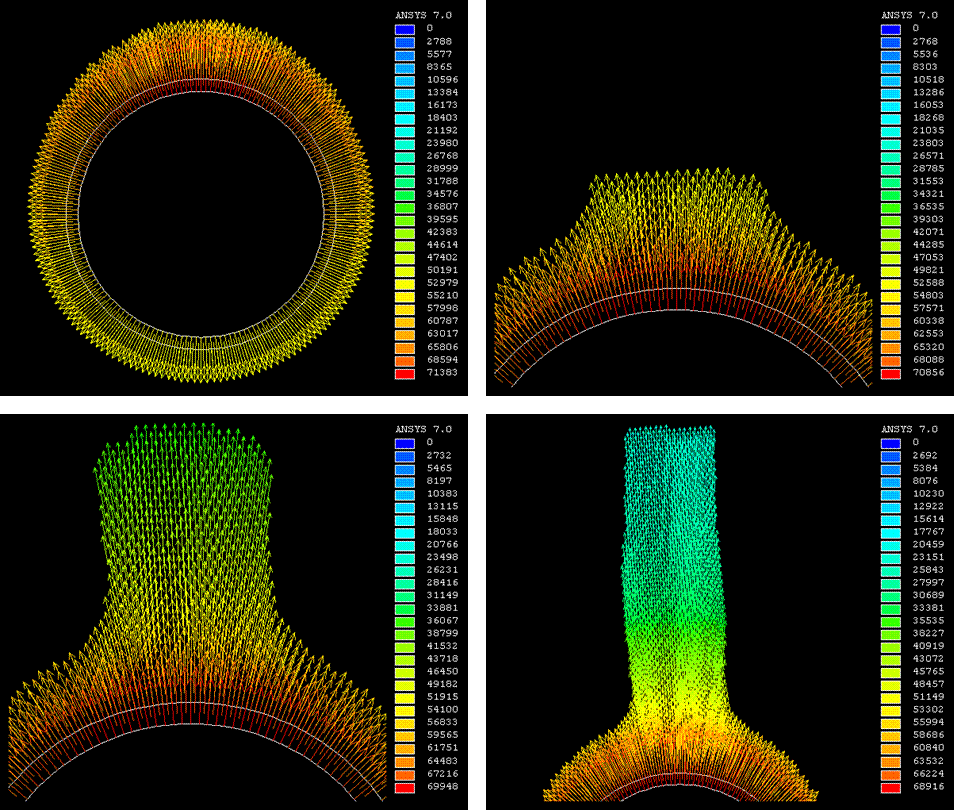
Рис. Динамика изменения кулоновских сил
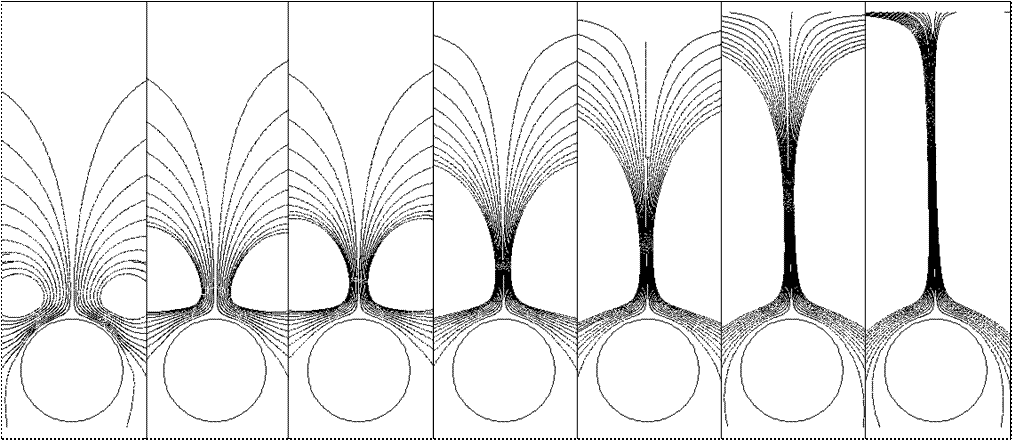
Рис. Сужение линий тока по мере распространения заряда к центру межэлектродного промежутка.
При выборе достаточно малого шага по времени между итерациями заряд не успевает расходиться в стороны по линиям тока за одну итерацию, а на следующей итерации новые силы сужают струи и заряд продолжает распространяться строго параллельно линии, соединяющей электроды. Таким образом, в представленной модели ЭГД-течение формируется в результате образования заряженной центральной струи, переносящий заряд в межэлектродный промежуток. Центральная струя в свою очередь образуется путем сноса ЭГД-течением заряда из первоначально сформированной кольцевой заряженной области. Считалось, что плотность заряда, возникающая у каждого из электродов одинакова, равна 0,01 C/m3 и соответствует знаку полярности электрода. Рассмотреть вопрос об изменении плотности заряда при сужении струи*
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.