Моделирование структуры ЭГД-течений в несимметричной системе электродов, страница 2

Классические задачи гидродинамики включают: обтекание тел, либо течения в трубах. ЭГД-течения – это течения с объемной нагрузкой. Такого рода течения исследованы недостаточно. Поэтому перед тем как решить гидродинамическую задачу с распределенной нагрузкой в виде силы, равной произведению плотности объемного заряда на напряженность электрического поля, было решено рассчитать более простой вариант, в котором распределение сил однородно в заданной области. Этот расчет позволит сделать общие выводы о структуре течений с объемной нагрузкой, получаемом при моделировании в конечно-элементном пакете. Таким простым вариантом является гидродинамическая задача с нагрузкой в виде прямоугольной области в центральной части межэлектродного промежутка, на рис 13 эта область выделена, в которой задается сила равная константе и направленная к плоскому электроду. Такое распределение силы в виде полоски было выбрано из следующих соображений. При развитом ЭГД течении с большим значением электрического числа Рейнольдса, заряд, образующийся у круглого электрода при движении к плоскому, не успевает расплыться в направлении перпендикулярном движению. Поэтому область локализации заряда имеет форму полоски шириной равной диаметру электрода. Реальное распределение сил в заданной области сложно, еще сложнее выявить соответствие его с распределением скоростей в кювете. Поэтому на первом этапе задавалось однородное распределение сил и моделировалось течение с таким распределением.

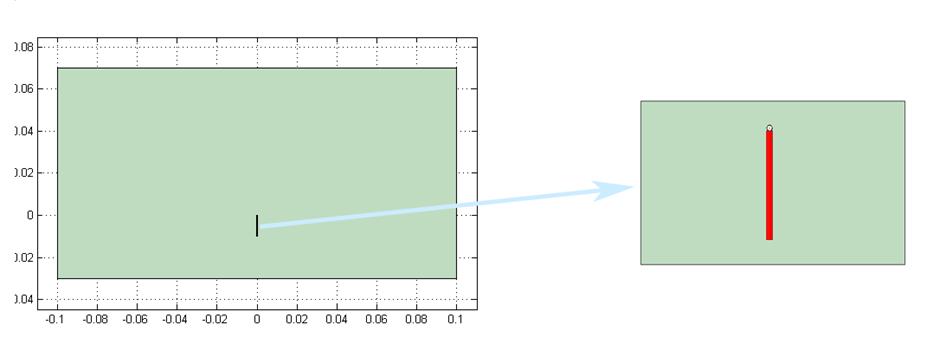
рис 13. Геометрия задачи для гидродинамической задачи.

 Красная полоска – область задания силы.

Для полной постановки задачи остается задать граничные условия. На всех стенках кюветы и поверхности круглого электрода задаётся нулевая скорость жидкости.

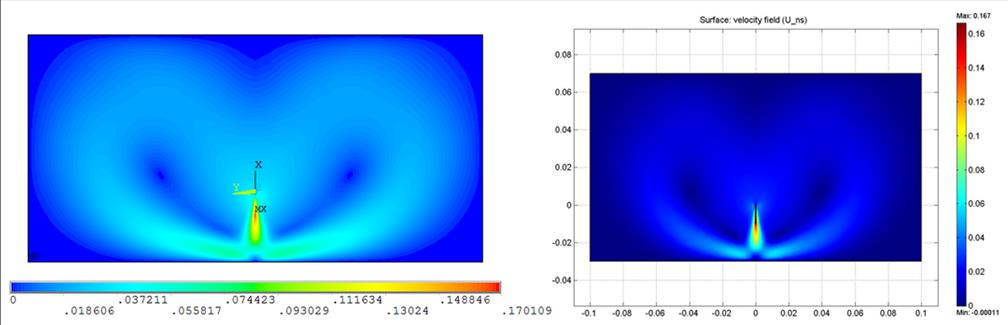
После решения модельной задачи с однородным распределением сил в области интереса получаем следующие результаты:

рис 14. Распределение скоростей в кювете.

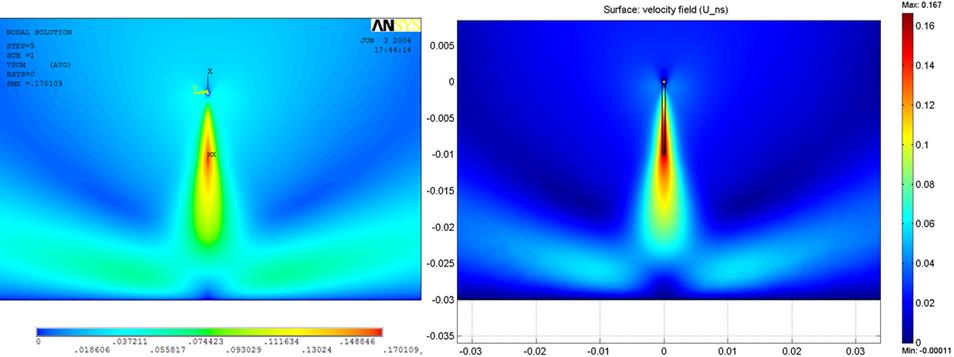рис 15. Увеличенное изображение распределения скоростей в

межэлектродном промежутке.

По приведённым изображениям можно сделать выводы об идентичности гидродинамических решений полученных в различных конечно-элементных пакетах. Течение с объемной нагрузкой представляет собой узкую струю, направленную от круглого электрода к плоскому и имеет ламинарный параллельно-струйный характер, что подтверждено на рис 16. Имеет зонную структуру: можно легко выделить неподвижные области около электродов, зону ускорения и зона торможения. Максимум скорости соответствует концу полоски, то есть точке окончания действия объемной силы. Это утверждение нарушится, если длина полоски будет близка к величине межэлектродного промежутка.

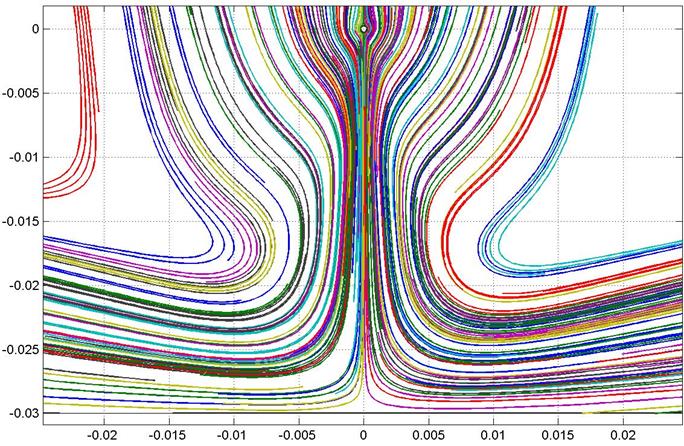рис 16. Линии тока в межэлектродном промежутке

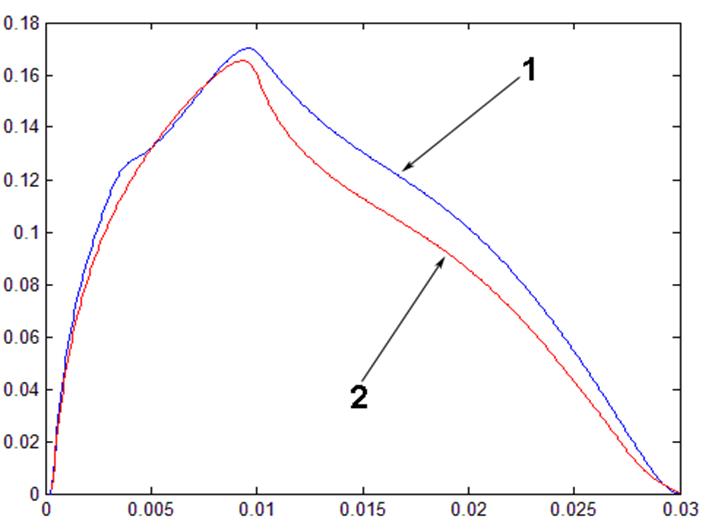
Аналогично с электростатической задачей были построены осевые распределения для скорости. Как ожидалось, струя состоит из двух зон: зоны разгона и зоны торможения. Причём граница зоны разгона находится в точке прекращения действия силы, она же соответствует точке максимальной скорости жидкости. Далее следует зона торможения жидкости.

Рис 17. Осевые распределения скоростей.

Ansys – синий график; Femlab – красный;

Во время расчетов были рассмотрены разные варианты длины полосы действия силы, результаты представлены на рис 18.

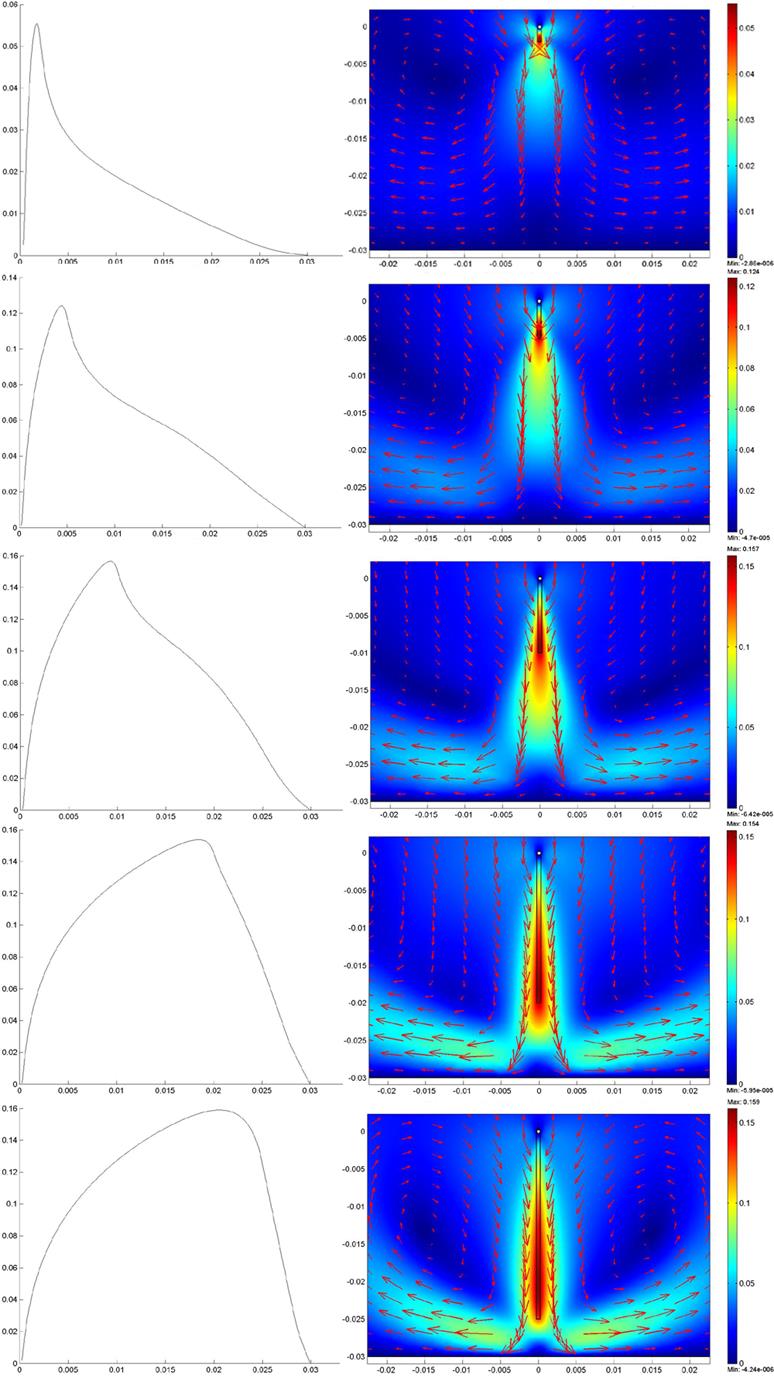Рис 18. Различные варианты длины области действия силы.

Слева – осевые распределения, справа – контурный график с векторным полем.

Как видно при изменении длины области действия силы, структура, описанная выше, не нарушается. Сохраняется зонная структура. Изменяется только максимальная скорость, значение которой растёт вместе с увеличением длины области действия силы, но данный рост прекращается при условии, что точка максимальной скорости близка к плоскому электроду. Стоит отметить, что все рассмотренные течения имеют Гауссов профиль, приведённый на рис 19.

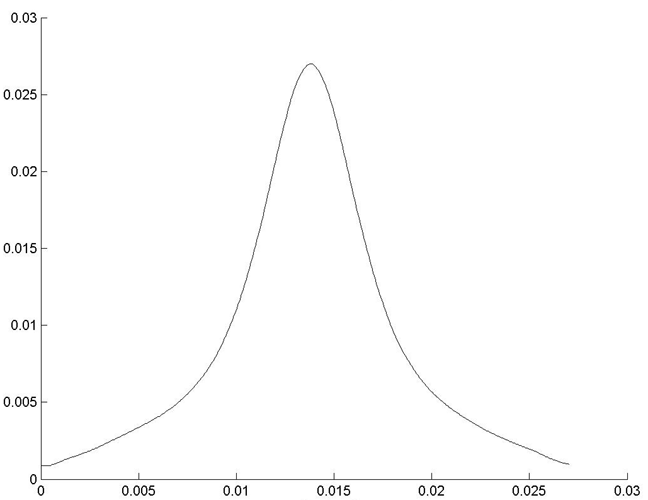рис 19. Профиль скорости