Физика \ Электрогидродинамика

Моделирование структуры ЭГД-течений в несимметричной системе электродов, страница 11

Как видно из этого выражения, параметр α  определяет ширину заряженной полоски.  Параметр β характеризует изменение заряда струи в процессе пересечения межэлектродного промежутка. Авторами были проведены специальные численные эксперименты для определения параметров α и β [5]. Оказалось, что для жидкостей с электрической проводимостью 0.1-1∙10-12 Ом-1∙м-1, для активного электрода с радиусом 0.25 мм параметр β равен 0.006, параметр α имеет значение 1∙10-4. В связи со сказанным выше, можно предположить, что при изменении радиуса активного электрода значения этих параметров не изменяются.

После определения граничных условий и распределения объемного заряда рассчитывалось распределение электрического потенциала в системе с помощью конечно-элементного пакета ANSYS, а затем определялось распределение напряженности элек

 


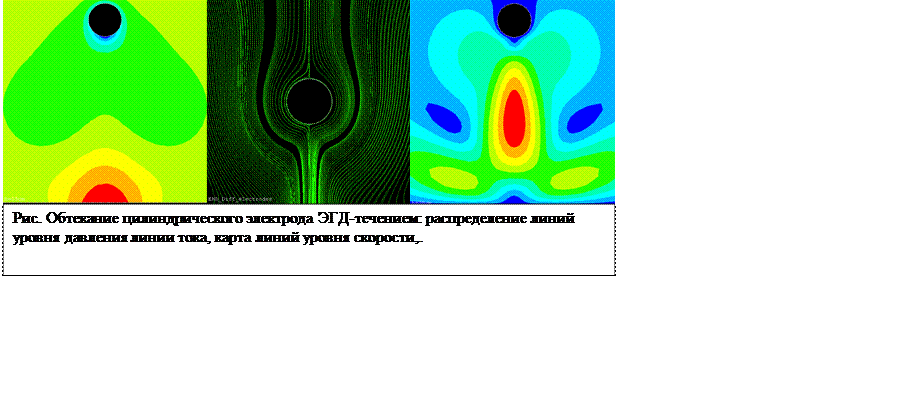трического поля, а также поле кулоновских сил. Найденное распределение плотности электрических сил использовалось в качестве внешних действующих сил в уравнениях гидродинамики. Граничными условиями были нулевые скорости на электродах и стенках кюветы. Геометрия электрической и гидродинамической частей задачи, а также свойства жидкости оставались постоянными и соответствующими условиям эксперимента. Гидродинамическая часть задачи также рассчитывалась при помощи метода конечных элементов в пакете ANSYS.

После вычисления, распределения скоростей сравнивались с результатами обработки экспериментальных данных и величина объемного заряда в приэлектродной области (ρ0) корректировалось в соответствии с экспериментальным значением скорости ЭГД течения для данных условий.

Результаты моделирования. Были проведены вычисления для нескольких электродов, радиусы которых менялись в пределах от 0.1 мм до 5 мм, таким образом напряженность электрического поля вблизи него менялась в пределах от 0.2·107 до 108 В/м. В результате решения электрической и гидродинамической задач получена полная информация об электрической и гидродинамической структуре ЭГД течений в развитом режиме от электродов различного диаметра при униполярной инжекции.

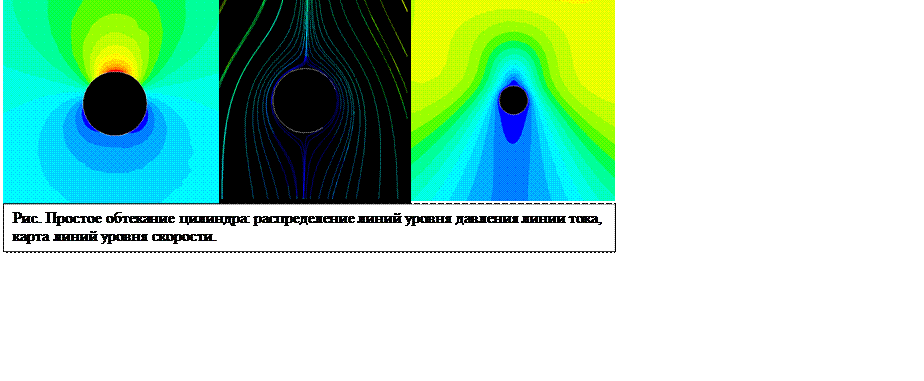
Полученные векторные поля скоростей и линии тока близко соответствуют фотографиям ЭГД течений полученным ранее, а также результатам обработки соответствующих видеофильмов [5]. На рис.1 приведены линии тока ЭГД течения в окрестностях активного цилиндрического электрода. Видно, что обтекание электрода имеет безотрывный характер, линии тока за электродом сходятся, образуя тонкую струйку. Линии тока в ней  параллельны центральной силовой линии электрического поля. Непосредственно к поверхности электрода примыкает приэлектродный слой, в пределах которого плотность электрического заряда и плотность кулоновских сил наиболее высока,  а скорость ЭГД течения очень мала. Жидкость, обтекая электрод, сносит заряд из этой зоны вглубь межэлектродного промежутка  в виде тонкой полоски. 

 В результате моделирования мы имеем полную информацию о течении и, благодаря этому, можем посчитать конвективную составляющую электрического тока Jk. Некоторые из полученных при моделировании результатов представлены в таблице 1.

Таблица 1.

r, мм

Reэл

Vmax, см/с

E·107 В/м

r0·10-2, Кл/м3

J1·10-6 А/м2

lm,мм

Am, м/с2

0.03

21.7

28.93

8.1

2.35

4.170

0.15

60.88

0.1

18.5

24.6

3.09

1.72

2.629

0.31

23.0

0.25

16

21.33

1.45

1.28

1.749

0.53

13.33

0.5

14.2

18.9

0.85

1.02

1.264

0.68

8.23

1

12.3

16.4

0.52

0.81

0.920

0.90

4.90

2

10.5

14

0.33

0.61

0.669

1.20

2.86

5

8

10.7

0.22

0.28

0.355

2.25

1.27
Скачать файл