Метод конечных элементов. Соотношения, определяющие элементы. Основные гипотезы теории упругопластических деформаций

1.  ВВЕДЕНИЕ

Метод конечных элементов (далее МКЭ ) является численным методом решения дифференциальных уравнений различных прикладных технических задач. Своим возникновением метод обязан исследованию физических явлений,  для которых аналитическое выражение слишком сложно и/или получение его требует огромных усилий. Конечно, применение метода, являющим собой лишь аппроксимацию точного решения, дает погрешность вычислений, однако, чаще всего, это связано с недооценкой физической природы исследуемого процесса.

Как инструмент анализа МКЭ характеризуется следующим образом:

1)  Физическая область задачи делится на подобласти, или конечные элементы.

2)  Зависимая переменная (одна или несколько) аппроксимируется функцией специального вида на каждом конечном элементе и, следовательно, во всей области. Параметры этих аппроксимаций в последующем становятся неизвестными параметрами задачи.

3)  Подстановка аппроксимаций в определяющие уравнения (или эквивалентные им) дает систему множества уравнений с неизвестными параметрами. Решая эти уравнения , можно получить значения этих параметров и, следовательно, определить приближенное решение задачи.

В данной работе для анализа состояний исследуемого объекта используется двумерный четырехугольный кубичный элемент, имеющий 12 точек интегрирования.

Работа с элементами осуществляется в естественной системе координат, поскольку она обладает определенным преимуществом при рассмотрении двумерных элементов, так как  позволяет деформировать границы этих элементов.  Интерполяционный полином для такого элемента имеет вид:

j = a₁+a₂x+a₃h+a₄xh+a₅x²+a₆h²+a₇x²h+a₈xh²+a₉x³+a₁₀h³+a₁₁x³h+a₁₂xh³, 

где x и h - естественные координаты изменяющиеся в пределах

-1£x,h³1.

Вычисление матрицы градиентов и переход к глобальной системе координат осуществляется так:

ëdN_b/dx  dN_b/dhû^T=[J] ëdN_b/dx   dN_b/dyû^T,

где [J]-матрица Якоби

       é dx/dx     dy/dx   ù

    [J] =½                            ½   .

       ë  dx/dh     dy/dh û

Преобразование координат выполняется по формулам:

x=R₁X₁+R₂X₂+…+R_nX_n

          y=R₁Y₁+R₂Y₂+…+ R_nX_n             .

Здесь Х,Y- координаты узлов на сторонах элемента в порядке их локальной нумерации 1¸n,  а R_b-функции для описания геометрии элемента.

                        2. СООТНОШЕНИЯ, ОПРЕДЕЛЯЮЩИЕ ЭЛЕМЕНТЫ

Чтобы получить соотношения, определяющие элемент, необходимо вычислить объемные и поверхностные интегралы:

[k^(e)]=ò_V[B]^T[С][B]dV.

Замену переменных интегрирования можно сделать с помощью соотношения

dV=t|det[J]|dhdxdV,

где t-толщина элемента. Объемные интегралы приводятся к виду

                                                            1  1

ò_V[B]^T[C][B]dV=tò  ò  [B]^T[C][B]|det[J]|dhdx,

                                                           -1 -1

где:

В=[D]([N]{U}), применение дифференциального оператора к матрице функций форм;

[С] - матрица упругих констант;

{U} - узловые значения функции     

Элементарные размеры равны:

dV=|det{J}|*2*pRdxh,   причем      J=]N]*]X,Y].

Якобиан отражает градиент искажения исходной геометрической формы элемента в локальных координатах x,h при его изображении в общей системе координат. Якобиан используется и для связи производных в разных системах отсчета

                                                1                 n_s 

Р_s=ò_s[N]^Tq_sdS=å [N]^T q_sdet[J]dx.

                                               –1                1

Переход к переменным интегрирования x и h упрощает пределы интегрирования, что позволяет избежать трудностей, возникающих при рассмотрении элементов с криволинейными границами.

Объемные интегралы записываются в общем виде следующим образом:

                                                           1  1

Z=ò  ò f(z,h)dhdx.

                                                          -1 -1

Этот интеграл может быть определен численно: сначала вычисляется внутренний интеграл, в котором x считается постоянной, а затем вычисляется внешний интеграл. Вычисление внутреннего интеграла дает:

                                              1                 n

òа(x,h)dh=åH_jf(x,h_j)=g(z),

                                             -1               j=1

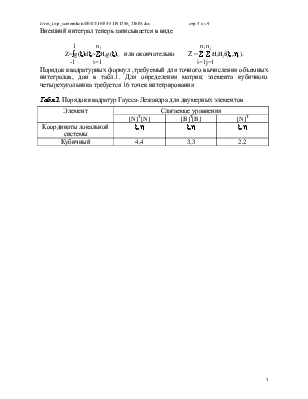
Внешний интеграл теперь записывается в виде

                    1            n_i                                                            n_i n_j

Z=òg(x)dx=åH_ig(x),   или окончательно        Z = å å H_iH_jf(x_i,h_j).