2. ТРЕУГОЛЬНЫЙ ЭЛЕМЕНТ
Каждая координатная компонента для треугольного элемента представляет собой отношение расстояния от выбранной точки до одной из сторон треугольника к высоте, опущенной на ту же сторону. Координаты треугольника обозначаются через L1, L2 и L3. Эти три величины не являются независимыми, они связаны между собой соотношением
L1+L2+L3=1 (1)
Каждому типу треугольных элементов соответствует интерполяционный полином определенного порядка. Квадратичный треугольный элемент, например, содержит шесть узлов (фиг. 1); интерполяционный полином для него имеет вид
j=a1+a2 x+a3 y+a4 x2+a5 x y+a6 y2. (2)
Величина ai в формулах (2) может быть определена методами, изложенными в гл. 3. Алгебраические операции при этом, однако, становятся более сложными, так как число узлов возрастает. Более предпочтительным оказывается, непосредственное получение функций формы. Использование естественной системы координат значительно упрощает эту операцию в случае
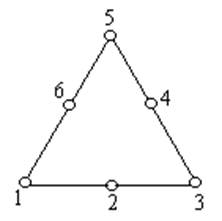
Фиг. 1, квадратичный элемент.
треугольного элемента. Мы начнем обсуждение треугольных элементов высокого порядка с рассмотрения непосредственного получения функций формы.
2.1.Функции формы для элементов высокого порядка
Общая формула для вычисления функции формы имеет вид
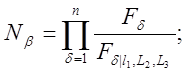 (4)
(4)
где n-порядок треугольника, а Fd-функции от L1, L2 и L3.Порядок треугольника
n определяется как величина , на единицу меньшая числа узлов на стороне треугольника .Квадратичный треугольник имеет три узла на стороне и поэтому является элементом второго порядка .
Функция Fd определяются из уравнений п линий, которые проходят через все узлы, за исключением узла, для которого определяется функция формы. Если рассматривается уравнение прямое L1=c , то Fd=L1-с. Знаменатель (4) есть значение Fd, определяемое с помощью координат узла b (узла, в котором вычисляется Nb).
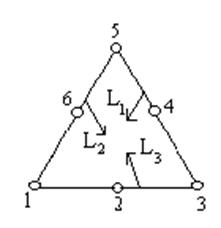
Фиг. 2. Функции формы для квадратичного элемента
N1=L1( 2 L1-1), N2=4 L1 L2 , N3=L2( 2 L2-1),
N4=4 L2 L3 , N5=L3( 2 L3-1) , N6=4 L1 L3;
2.2.Вычисление производных функций формы
В качественезависимых координат выберем координаты L1 и L2 . Дифференцируя получаем
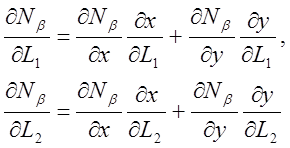 (5)
(5)
Матрица Якоби имеет вид
![]()
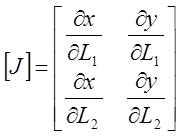 (6)
(6)
Поэтому
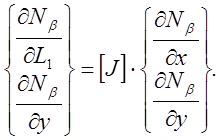 (7)
(7)
Таким образом, для производных получаем
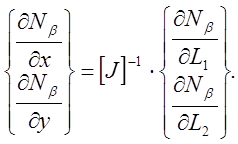 (8)
(8)
Чтобы учесть зависимую координату L3, можно поступить двояко: либо переписать все функции формы, выразив их через L1 и L2 , либо заметить, что
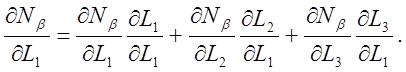 (9)
(9)
Производная ¶L1/¶L1 равна единице, a ¶L2/¶L1 равна нулю, так как L1 и L2 независимые. Третье слагаемое может быть вычислено с помощью соотношения
L3=1-L1-L2. (10)
Дифференцируя его, имеем
¶L3/¶L1=-1.
Теперь формула (9) преобразуется к виду
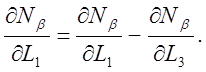 (11а)
(11а)
Аналогичное выражение получаем для ¶Nb/¶L1:
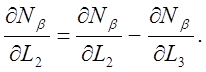 (11б)
(11б)
Принятые в формулах (11a) и (116) обозначения могут сначала вызвать недоумение, потому что члены ¶Nb/¶L1 и ¶Nb/¶L2 находятся в обеих частях равенства. Частная производная от Nb в левой части равенств вычисляется, когда Nb выражена как функция независимых координат L1 и L2. В правой части функция N считается выраженной через L1 ,L2 ,L3 .
Соотношения преобразований координат, определяющие форму элемента, обычно записываются с использованием трех координат. Следовательно, при вычислении матрицы Якоби должны применяться формулы (11а) и (116).
Применение сформулированных выше положений иллюстрируется на следующем примере.
Требуется вычислить ¶N4/¶xв точке (1, 4) для квадратичного треугольного элемента, показанного ниже.
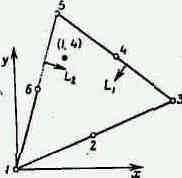
Форма элемента может быть задана с помощью линейных функций формы L1, L2 и L3 и координат узловых точек, расположенных в вершинах треугольника. Запишем формулы преобразований координат
X=L1X1+L2X2+L3X3,
Y=L1Y1+L2Y2+L3Y3.
После подстановки узловых координатимеем
X=3L2+L3,
Y=2L2+6L3.
Вычислим производные, входящие в матрицу Якоби:
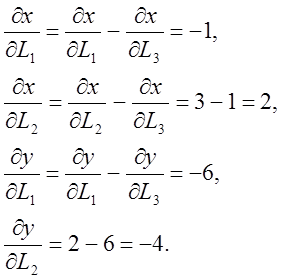
Матрица Якоби и обратная к ней матрица имеют вид
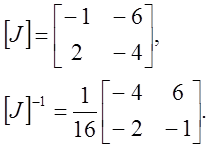
Функция формы N4 есть 4L2 L3. Дифференцируя ее по L1 и L2,
получаем
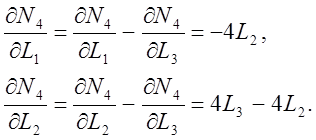
Подстановкаэтих частных производных вместе с [J]-1 в формулу (8)
дает
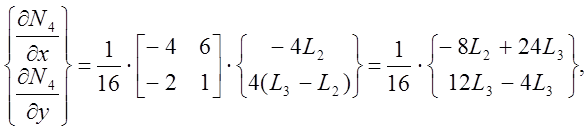
или
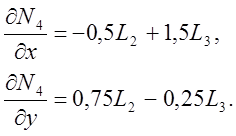
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.