Изучение безвихревого течения идеальной жидкости

2.1.1.Кубичный четырёхугольный элемент.

  До сих пор применение метода конечных элементов были связаны с использованием одномерных линейных элементов , двумерных треугольных элементов и трёхмерного тетраэдра . Теперь рассмотрим новую группу элементов: двумерный четырёхугольник.

  Четырехугольный элемент представляет собой мультиплекс-элемент . Границы такого элемента должны быть параллельны координатным линиям для сохранения непрерывности при переходе от одного элемента к другому. Прямоугольный элемент является специальным случаем четырёхугольника . Свойства прямоугольного элемента служат основой для применения криволинейной системы координат, необходимой при использовании четырёхугольного элемента .

  Рассмотрим четырехугольный элемент, содержащий 12 узлов. Такой элемент называются соответственно кубичным элементом, так как его интерполяционный полином является кубичной функцией вдоль линий x=const и h=const.

  Интерполяционный полином соответственно для кубичного элемента (рис.2.1) записывается в виде

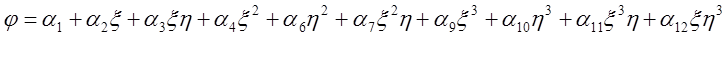(2.1).

                                     

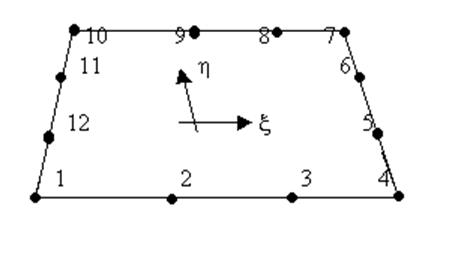
Рис.2.1. Кубичный четырехугольный элемент.

Функции формы для этого элемента представляют собой полиномы , идентичные по форме (2.1). Функции формы для двумерных элементов равны нулю во всех узлах , за исключением узла , номер которого совпадает с номером соответствующей функции формы; кроме того , они принимают узловые значения вдоль всех границ элемента , которые не содержат указанного узла . Например , функция формы N₁ для элемента (рис.2.1 ) обращается в ноль во всех узлах , за исключением первого узла .

  Функции формы могут быть непосредственно получены комбинированием функций , которые обращаются в нуль на границах элемента . Множество функций , равных нулю  вдоль одной из сторон элемента , легко получить из функций формы для линейного четырёхугольника . Произведение любых двух таких функций  соответствует первым членам в формуле (2.1) . Поэтому удобно записать функции формы в виде произведения двух полиномов :

 (2.2)

Остановимся теперь на определении постоянных, входящих в последние соотношения. В качестве базисных функций выберем следующие:

f₁=(1+h),

                             f₂=(1-x),                      (2.3)

f₃=(1-h),

f₄=(1+x).

Каждая из них обращается в нуль на одной из границ элемента.

  Введем еще множество функций F_i , i=1, 2, 3, 4:

              f_k , если узел b не принадлежит стороне k ,

 F_k=              k=1,2,3,4,                                                             (2.4)

              1 ,если узел b принадлежит стороне k .

Функция формы для кубичного элемента дается формулой

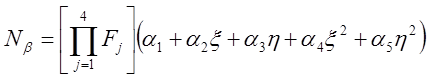     (2.5)

Степень многочлена в (2.5) определяется числом имеющихся узловых условий. Его коэффициенты определяются приравниванием N_b единице в узле b и нулю во всех других узловых точках, которые не входят в произведение .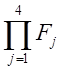

2.1.2.Определение функций формы .

  Рассмотрим определение функции формы N₂ для элемента, показанного на рис.2.1.

  Узел 2 принадлежит первой стороне элемента, поэтому F₁=1. Остальные три функции следующие: F₂=f₂=(1-x), F₃=f₃=(1-h) и F₄=f₄=(1+x).Произведение в (2.5) равно

 .

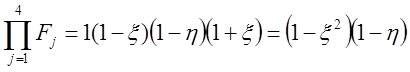Общее выражение для N₂ имеет вид

N₂=(1-x²)(1-h)(a₁+a₂ x+a₃h+a₄x²+a₅h²).

Полином, содержащий произвольные константы, должен быть усечён, так как не выполнены всего два узловых условия

N₂=1 при x= -1/3 , h= -1

 и

N₂=0 при x=1/3 , h= -1.

Коэффициенты a₄ и a₅ должны быть вычеркнуты, поскольку члены вида x⁴ и x²h² не входят в формулу (2.1) . Сохранение члена a₃h приводит к системе уравнений с нулевым определителем, поэтому этот член тоже должен быть зачёркнут. Таким образом, для N₂ имеем

N₂=(1-x²)(1-h)(a₁-a₂x).

Используя условия в узлах, получаем систему

(1-1/9)2(a₁-a₂/3)=1,

(1-1/9)2(a₁+a₂/3)=0,

откуда находим a₁=9/32 и a₂= - 27/32. Окончательное выражение для функции формы имеет вид

N₂=9/32(1-x²)(1-h)(1-3x).

  Приведём     расчёт значений функций формы для кубичного элемента (рис.2.1):

         

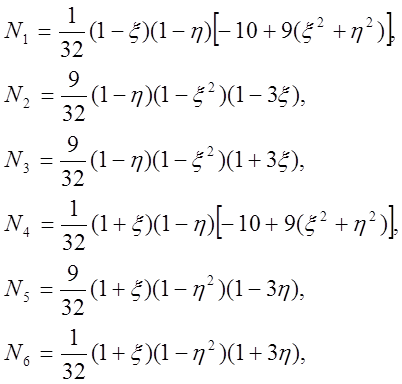
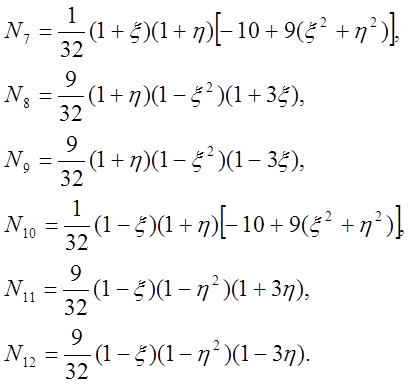
Простым сложением можно убедиться, что эти функции формы удовлетворяют критерию 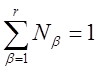  для элемента.

2.1.3.Вычисление производных функций формы.

 Матрица Якоби определяется соотношением

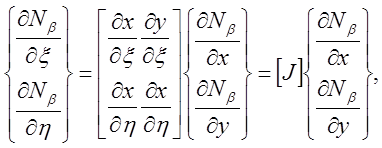  (2.6)

которое можно обратить, чтобы получить частные производные, по x и по у.

  Матрица Якоби является функцией x и h даже для простейших четырехугольных элементов. Эта зависимость легко обнаруживается при рассмотрении преобразования координат:

x=R₁C₁+R₂C₂+R₃C₃+R₄C₄ ,(2.6)

где C₁ ,C₂ ,C₃ ,C₄¾x-координаты четырех вершин. R_b используется здесь для обозначения функций, определяющих форму элемента. Дифференцируя x по x, получаем

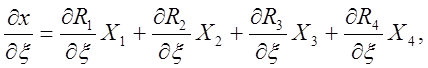
где

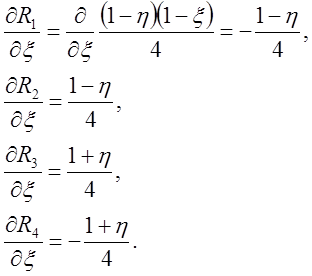(2.7)

После подстановки и перемножения имеем

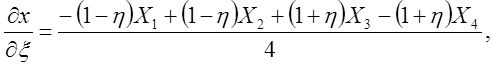
Отсюда видно, что коэффициенты матрицы [J], являются функциями x и h.

   Определим частные производные  и  .