Изучение безвихревого течения идеальной жидкости, страница 3

     1. Компоненты вектора поправок d^(p) удовлетворяют неравенству

   (i=1,2,3,…..N) ,

в этом случае X=X^(p) выдаётся в качестве решения.

     2. Предположим, что при p>1 для некоторых i предыдущее неравенство нарушается, но выполнено следующее:

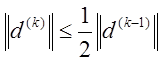  (k=1,2,3,…..,p-1);

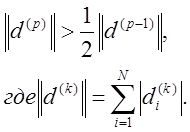
   Тогда, если , то заданной точности удовлетворяет только норма полученного решения.

    Если , то норма полученного решения не удовлетворяет заданной точности.

     3. 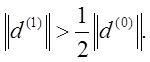 В этом случае полученное решение далеко от точного решения и итерационный процесс не сходится, что в общем случае означает плохую обусловленность матрицы А.

     4. U ¾ особенная матрица.

     Во всех случаях выдаётся X=X^(p).

     Обращение к подпрограмме имеет вид

CALL RSLMC (A,AF,B,X,N,ESI,IER,IA,V,PER)

       A ¾ массив, содержащий элементы исходной матрицы (точность обычная);

       AF  ¾ массив, содержащий элементы двух треугольных матриц, на которые разлагается исходная матрица (точность обычная);

       B ¾ массив, содержащий элементы вектора правых частей системы (точность обычная);

       X ¾ массив, содержащий вычисленное решение системы уравнений (точность обычная);

       N ¾ порядок системы;

       EPSI ¾ относительная погрешность вычислений (точность обычная);

       IER ¾ индикатор ошибок, который может принимать следующие значения:

            IER=0, если каждая компонента X удовлетворяет заданной точности;

            IER=1, если только норма X удовлетворяет заданной точности;

            IER=2, если точность нормы вычисленного решения меньше заданной                   точности;

            IER=3, если полученное решение вообще не имеет смысла;

            IER=4, если какой-нибудь диагональный элемент верхней треугольной матрицы равен нулю;

       IA ¾ граница первого измерения, указанная для массива A в вызывающей программе, если исходная матрица хранится в форме с двойной индексацией. Если матрица хранится в векторной форме, то IA=N;

       V ¾ рабочий массив длиной большей или равной N;

        PER  ¾ массив длиной N, содержащий перестановку строк исходной матрицы.

   Приведем описание подпрограммы RSLMC:

      SUBROUTINE RSLMC (A,AF,B,X,N,EPSI,IER,IA,V,PER)

      DIMENSION A(1),AF(1),B(1),X(1),V(1),PER(1)

      DOUBLE PRECISION DP

C

C        INITIALIZATION

C

      D0=0.

      IER=0

      ITE=0

      DO 10 I=1,N

      V(I)=B(I)

   10 X(I)=0.

   20 ITE=ITE+1

C

C        THE PERMUTATIONS OF ROWS OF A ARE APPLIED TO V

C

      DO 30 I=1,N

      K=PER(I)

      IF (K-I)25,30,25

   25 D1=V(K)

      V(K)=V(I)

      V(I)=D1

   30 CONTINUE

C

C        SOLUTION OF THE LOWER TRIANGULAR SYSTEM

C

      DO 50 I=2,N

      IM1=I-1

      DP=V(I)

      IK=I

      DO 40 K=1,IM1

      DP=DP-1.D0*AF(IK)*V(K)

   40 IK=IK+IA

   50 V(I)=DP

C

C        SOLUTION OF THE UPPER TRIANGULAR SYSTEM

C

      IF(AF(IK)) 58,54,58

   54 IER=4

      GO TO 82

   58 V(N)=DP/AF(IK)

      DO 70 I=2,N

      IM1=N-I+1

      INF=IM1+1

      DP=V(IM1)

      IK=(IM1-1)*IA+IM1

      D1=AF(IK)

      DO 60 K=INF,N

      IK=IK+IA

   60 DP=DP-1.D0*AF(IK)*V(K)

   70 V(IM1)=DP/D1

C

C        TEST OF PRECISION

C

      D1=0.

      D2=0.

      KLE=0

      DO 80 I=1,N

      D1=D1+ABS(V(I))

      D2=D2+ABS(X(I))

      IF (ABS(V(I))-EPSI*ABS(X(I))) 80,80,75

   75 KLE=1

   80 CONTINUE

      IF (KLE)140,82,85

   82 RETURN

   85 IF (ITE-1)140,90,87

C

C        ITERATIONS ARE STOPPED WHEN THE NORM OF THE CORRECTION IS MORE

C        THAN HALF OF THE ONE OF THE FORMER

C

   87 IF (D0-2.*D1)120,90,90

   90 DO 95 I=1,N

   95 X(I)=X(I)+V(I)

      DO 110 I=1,N

      DP=B(I)

      IK=I

      DO 100 K=1,N

      DP=DP-1.D0*A(IK)*X(K)

  100 IK=IK+IA

  110 V(I)=DP

      D0=D1

      GO TO 20

  120 IF(ITE-2)140,140,125

  125 IF (D1-EPSI*D2)127,127,130

  127 IER=1

      RETURN

  130 IER=2

      EPSI=D1/D2

      RETURN

  140 IER=3

      RETURN

      END

3.Заключение

   В данной курсовой работе рассмотрено безвихревое течение идеальной жидкости потому, что на основе данной физической задачи могут быть решены многие другие, такие, как обтекание несущих поверхностей самолёта, различных конструкций и тому подобное.

   При выполнении работы был рассмотрен кубичный элемент, который связан с применением метода конечных элементов, и, в принципе, может быть использован в решении задачи течения, рассмотренной выше. 

   Описание программы в данной курсовой работе показывает возможность рационализации работы, при которой происходит реальная экономия времени.

4. Литература

1. Сегерлинд Л.Д., ”Применение метода конечных элементов”, Москва: Мир, 1979год.

 2. Лойцянский П.Г., “Механика жидкости и газа”, Москва: Наука, 1973 год.

 3. Кудряшов И.А., Кушнер и др., “Программирование, отладка и решение задач на ЭВМ единой серии. Язык Фортран.”