Учет несжимаемости материалов. Гибридные формулировки

 Учет несжимаемости материалов. Гибридные формулировки

Во многих расчетных случаях необходимы прочностные исследования твердых тел содержащих несжимаемую идеальную жидкость, либо материалов, обладающих свойством несжимаемости (коэф. Пуассона равным 0,5). Задачи такого типа представляют особый интерес в биомеханике, например, при анализе глазного яблока или межпозвоночных хрящей. В военной технике также используются сложные конструкции включающие наполнители, полимерные материалы, представляющие собой “начинку“ или содержимое из взрывчатых вещества различного рода, либо горючих материалов - твердого или жидкого топлив в тепловых двигателях ракет, торпед и т.д.

4.1. Учет несжимаемости жидкости

Метод, разработанный Германном [4.1,4.2] для несжимаемых материалов, в данном случае неэффективен с вычислительной точки зрения и громоздок, поскольку он требует, чтобы несжимаемый материал сопротивлялся сдвигу. В целях постепенного усвоения материала приведем один из методов анализа, а затем покажем существующий разработки.

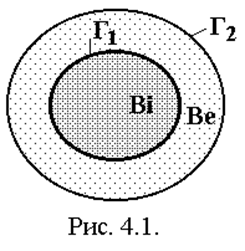
Рассмотрим систему [4.3] В, состоящую из несжимаемой идеальной сплошной среды Вi, заключенной в твердое тело Ве. Внутренняя поверхность обозначена через Г₁, а наружная — через Г₂ (Рис.4.1). Решения уравнений равновесия имеют вид

dI(u_i,p)=0                       (4.1)

         где      I=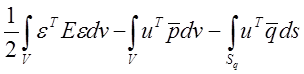     .   (4.2)

Здесь и_i — поле перемещений, совместное со связями, р — давление, e_ij и s_ij — тензоры деформаций и напряжений в декартовых координатах; Т_i — усилия, приложенные к поверхности. Варьируя по и_i и р и используя теорему Гаусса, получаем равенство

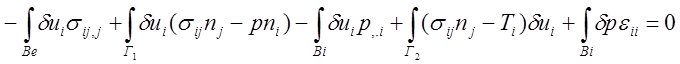(4.3)

которое включает соответственно условия равновесия Ве, на внутренней поверхности, в Вi, на Г₂, и условие несжимаемости. Здесь n_i — единичный вектор нормали, внешней по отношению к Ве.

Пусть Biи Be разделены соответственно на Ni и элементов, характеризуемых перемещениями узлов  {D} и силами {F}, сосредоточенными в узлах. Обозначая напряжения и деформации элементов через {s} и {e} для каждого элемента запишем уравнение линейной зависимости напряжений от деформаций в матричной форме:

                                                                     {e }=[E]{D}               .            (4.4)

Если твердое тело упруго, то в области Bi                {s }=[C]{e }              .            (4.5)

Условие несжимаемости можно записать в виде     {I } ^Т{e }=[I]^Т[E]{D}=0     .    (4.6)

Элементы {I }, связанные с нормальными напряжениями, равны единице, а остальные равны нулю. Условие равновесия состоит в том, что производные от р обращаются в нуль. В уравнении (4.3) в неявном виде предполагается, что давление является единственной неизвестной постоянной в Bi.

Функционал I выражаем через {D} иpследующим образом:

I=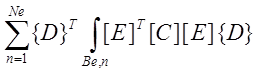+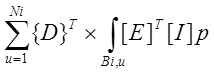- {D} ^Т{F} =0     .    (4.7)

Варьируя {D} иp, получаем следующие уравнения:

                    [K]{D}+p{T}={F}     .                                 (4.8)

                     {T}^T{D }=0       ,                                          (4.9)

где                                                       [K]=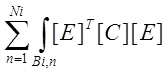     .                                (4.10)

                                                {T}=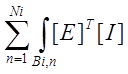     .                                    (4.11)

Уравнение (4.8) представляет условия равновесия, а уравнение (8.9) — условие несжимаемости. Уравне­ние (9) включает только узлы, внутренние и граничные но отношению к Ве, так как очевидно, что условие несжимаемости не зависит от перемещений узлов, внутренних по отношению к несжимаемой сплошной среде Bi.

Решение имеет вид 

p=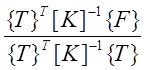                  .                        (4.12)

Следовательно                                       {D }=[K]^-1({F}-p{T})           .                       (4.13)

Решение этих уравнений несколько сложнее, так как оно требует одновременного решения с двумя нагрузками.

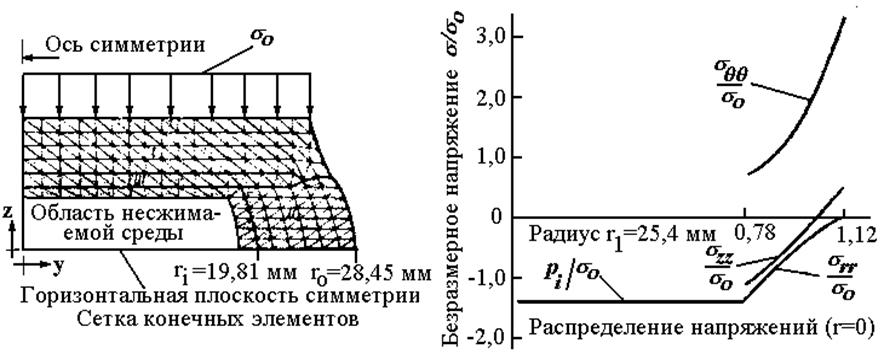Рис. 4.1. Результаты для межпозвоночного хряща

Приведенный подход при переходе к бесконечно малым приращениям можно использовать и для нелинейных материалов.

В качестве примера применения данного метода рассмотрим поясной межпозвоночный хрящ.  На Рис. 4.1, приведены результаты с использованием осесимметричной модели решения задачи. Материал характеризуется следующими свойствами:

Е_I = 27600 Н/см²,        n_I =0,25,         Е_III = 3450 Н/см²,      n_{I I I} =0.25,       s₀ = 5,18 Н/см²,