Учет несжимаемости материалов. Гибридные формулировки, страница 2

C_II=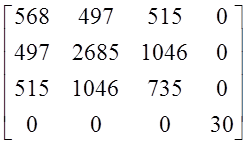H/см² .

Результаты расчетов согласуются с экспериментальными, отношение p_i/s₀постоянно в области несжимаемости жидкости и имеет значение, лежащее в пределах от 1 до 1,5; здесь получено 1,38. Отмечается, что выпучивание u [при r=2,84 см, z=0]  составляет 0,294 мм, а значение сжатия области II в вертикальном направлении составляет 0,109 мм. В расчетах получены значении 0,30 и 0,109 мм.

4.2. Особенности расчетных формулировок

Для более корректного учета особенностей такого рода, в отличие от подходов, использующих одно-полевые  вариационные формулировки функционалов только для перемещений или напряжений, приведем гибридные [4.4]. Так, вместо принципа виртуальных работ часто применяют классические смешанные экстремальные принципы.

1. Принцип минимума полной потенциальной энергии: среди всех допустимых перемещений упругого тела перемещения, соответствую­щие положению равновесия, сообщают функционалу полной потен­циальной энергии минимальное значение.

Полную потенциальную энергию представляют формулой

               П(u)=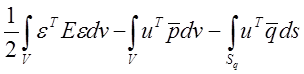,                (4.14)

Дополнительные условия:                  ed=Du,    u|_Su=u       .                          (4.15)

Условия минимума:       dП(u)=0;     d²П(u)³0;  П(u) ® к минимуму.(4.16)

2. Принцип минимума дополнительной работы (принцип Кастильяно): среди всех возможных напряженных состояний условиям рав­новесия соответствует то, которое придает функционалу дополнитель­ной работы минимальное значение.

Выражение для дополнительной работы (потенциал Кастильяно) имеет вид

                        П^*(s)= 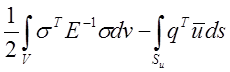,                    (4.17)

Дополнительные условия:                   D^Ts +=0;       q|_Su=.                      (4.18)

Условия минимума:         dП^*(s)=0;     d²П(s)³0; П^*(s)® к минимуму.(4.19)

Очевидна двойственность обоих принципов. Необходимыми усло­виями одной вариационной формулировки являются естественные ус­ловия другой.

Гибридный полный потенциал (в объеме варьируется полеи, на границе—значения q):

                         Пн(u,q)=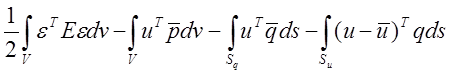,       (4.20)

dПн(u,q)=0,  Пн(u,q) ® к стационарному значению.

Сопряженный гибридный потенциал (в объеме варьируется полеs, на границе — значения u):

      Пн^*(u,s)=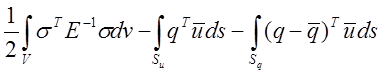,             (4.21)

dПн^*(u,s)=0, Пн^*(u,s)® к стационарному значению.

Если отдать предпочтение использованию величин одного какого-либо типа, то получим смешанные вариационные принципы, которые также могут быть сформулированы как гибридные. Геллингером и Рейснером предложен следующий смешанный вариа­ционный принцип:

                        П_R^*(u,s)=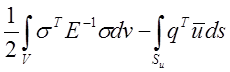  ,                   (4.22)

dП_R^*(u,s)=0, П_R^*(u,s)® к стационарному значению.

Соответствующие функционалу П_R(u,s) уравнения Эйлера — Лагранжа содержат статические и кинематические условия.

Смешанные вариационные принципы приводят к уравнениям тео­рии с более низким порядком производных, чем уравнения, получен­ные на основе классических вариационных принципов. Соответствен­но ослабляются и требования к гладкости допускаемых к варьирова­нию функций u и s.

Вариационный принцип Геллингера — Рейснера и различные его модификации (включая гибридные) являются принципами стационар­ности, для которых свойства максимальности или минимальности не удовлетворяются. Принцип Геллингера — Рейснера можно вывести обобщением принципа минимума полной, потенциальной энергии.

Гибридные вариационные формулировки чаще всего используются для исследований пластинчатых и оболочечных конструкций.

ЛИТЕРАТУРА

К разделу 4.1

4.1.  Германн Л.Р., Томс. Преобразование уравнений поля перемещении упругой среды к новой форме, пригодной для всех допустимых значений коэффициента Пуассона..// Журн. Прикладная механика, №1, 1964, стр. 166. нзд-во «Мир».

4.2.  Германн Л.Р., Кэмпбелл Д.М. Метод дискретных элементов для тонких оболочек.— Ракетная техника и космонавтика, 1968, № 10.

4.3.  Беличко Т., Кулак Р. Метод конечных элементов для твердого тела содержащего идеальную несжимаемую жидкость.//Журн. Ракетная техника и космонавтика, 1973, т.4,№9, с. 296-297.

К разделу 4.2

4.4.  Сахаров А.С., Кислоокий В.Н., Киричевский В.В., Альтенбах И., Габберт У. И др. Метод конечных элементов в механике твердых тел. //Под ред. А.С. Сахарова, И.А. Альтенбаха. –Киев: Выща школа, 1082г. –480с.

4.5.