Треугольный элемент. Функции формы для элементов высокого порядка. Вычисление производных функций формы. Программа MCHB, страница 2

Эти два соотношения выполняются в произвольной точке элемента. Наша цель—определить производные в точке (1, 4). Для дости­жения этой цели следует определить L-коордннаты данной точки. Используя преобразования координат, можно записать

1=0L₁+3L₂+ L₃,

4=0L₁+2L₂+6L₃,

1=L₁+L₂+L₃.

  Решением этой системы являются числа

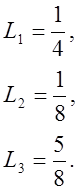
Подставляя значения L₂ и L₃ в формулы для производных, полу­чаем

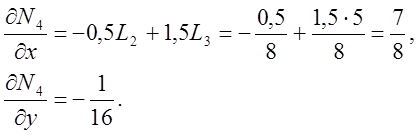
2.3.Составление матриц элементов

   Если интерполяционные соотношения содержат L-координаты, в уравнениях для элементов появляются интегралы по площади элемента следующего вида:

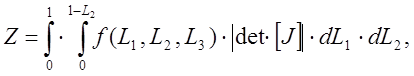                                   (12)

Эти интегралы должны быть определены численно, поскольку мат­рица Якоби является функцией L-координат и невозможно полу­чить явное выражение для обратной матрицы.  Однако использование этих формул услож­няется, тем, что, прежде чем приступать к почленному  интегриро­ванию требуется вычислить произведение матриц  Ошибок будет меньше, если эту операцию интегрирования выпол­нит ЭВМ.

      Процедура численного интегрирования аналогична той, которая была рассмотрена применительно к одномерному элементу.  Использование  интеграла (12) заменено суммой:

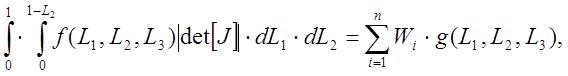                              (13)                                          

где g(L₁ ,L₂ , L₃) включая Порядок интерполирования определяется суммой показателей степеней трех координат в каждом члене .

3. Программа MCHB

Эта подпрограмма в зависимости от указанного при обращении режима работы позволяет произвести для заданной симметричной положительно определенной ленточной матрицы А порядка М и матрицы общего вида R размером М´N следующие операции:

             Разложение матрицы А в произведение треугольных множителей:

где Т_u-ленточная верхняя треугольная матрица;

         вычисление матрицы

         вычисление матрицы  ;

         вычисление матрицы  ;

         Матрица А разлагается  на множители по методу квадратных корней Холецкого.

Вычисление элементов верхней треугольной матрицы Т_u c учетом ее ленточной структуры производится по следующим формулам:

       (j=2,3,…,MUD+1);

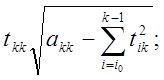     i₀=max{1,k-MUD}  (k=2,3,…,M);

   

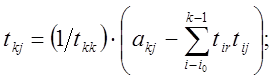
где MUD-число верхних кодиагоналей матриц А и Т_u.

          Вычисление  эквивалентно решению системы   и производится по формулам:

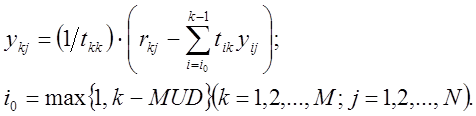
Аналогично вычисление  эквивалентно решению системы T_uX=R и осуществляется с помощью соотношений:

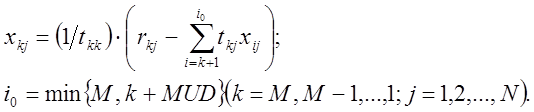
Вычисления А^-1R производится в два этапа . Сначала вычисляется значение  а затем .

              Обращение к подпрограммам имеет вид:

               CALL MCHB(R, A, M, N, MUD, IOP, EPS, IER)

              R-массив длиной M´N, содержащий при обращении к подпрограмме заданную матрицу R  общего вида размером M´N, расположенную по столбцам . При выходе из подпрограммы этот массив содержит элементы матрицы -результата в соответствии с заданным значением параметра IOP.При IOP=0 этот массив не используется.

               А-массив длиной M+MUD(2M-MUD-1)/2, содержащий при IOP=0,1,2,3 заданную симметричную положительно определенную ленточную матрицу А, а при IOP=-1,-2,               -3-ленточную верхнюю треугольную матрицу Т_u.Матрицы хранятся в уплотненном виде        (главная диагональ и MUD верхних кодиагоналей) по строкам. В тех случаях , когда исходной является матрица Т_u , она должна быть предварительно получена . При выходе из подпрограммы во всех  случаях этот массив содержит ленточную матрицу T_u , хранящуюся в уплотненном виде;

                М-число строк и столбцов матриц А и Т_u и число матрицы R;

                N-число столбцов матрицы R (в случаи IOP=0 заданное значение N не используется);

                MUD-число верхних кодиагоналей матриц А и Т_u ;

                IOP-параметр , управляющий режимом работы  подпрограммы : при IOP=0 производится разложение матрицы , т.е. вычисляется матрица T_u ; при IOP=3,

-3,-;

                EPS-переменная , значение которой используется как относительный допуск при проверке потери значимости (точность обычная) . Для подпрограммы MCHB значение EPS рекомендуется выбирать  в диапазоне 10^-7-10^-6 ;

                IER-индикатор ошибки:

                     IER=0 означает , что в процессе работы подпрограммы ошибок не было;

                     IER= -1 означает отсутствие результата по одной из следующих причин :

                     MUD<0 или MUD+1>M , или ABS[IOP]>3 ; на некотором шаге подкоренное выражение  неположительно ; появление нулевого диагонального элемента на одном из шагов деления;

                     IER=k-указывает на потерю точности , т.е. при разложении матрицы А в произведение треугольных матриц некоторое подкоренное выражение   оказалось положительным , однако меньше величины .Это может привести к потере значащих цифр результата вследствие потери значащих цифр при вычислении .