Метод конечных элементов. Соотношения, определяющие элементы. Основные гипотезы теории упругопластических деформаций, страница 4

    Компоненты напряжений должны удовлетворять дифференциальным уравнениям равновесия и условиям на поверхности тела, если на ней или ее части заданы напряжения. Заметим, что условия на поверхности тесно связаны s дифференциальными уравнениями. Их необходимо рассматривать совместно. Уравнения равновесия не могут иметь определенного решения, пока не даны условия на поверхности. Если дифференциальные уравнения и условия на поверхности удовлетворены, то это говорит о том, что все элементы тела как внутри его, так и у его поверхности находятся в равновесии. Следовательно, обеспечено и равновесие тела в целом.

  Условия совместности деформаций выражают отсутствие разрывов и непрерывность деформации тела.

   Требования к соблюдению столь большого числа условий приводит к тому, что многие задачи за пределами упругости до сих пор не имеют решения. Поэтому в теории пластичности еще в большей степени, чем в теории упругости, имеют значение приближенные методы решения. Наиболее приемлемым к (МКЭ) является метод переменных параметров упругости.

В основе этого метода лежит представление зависимостей деформаций от напряжений по теории упруго-пластических деформаций в форме так называемого обобщенного закона Гука, в котором параметры упругости зависят от напряженного состояния в точке и поэтому различны для различных точек тела.

  Используя соотношения

e=(1/E_P)(s-m_P(s+s))+Q

……………………….                                                                       (2.1)

g=t/G_P

где Q-температурная деформация, а E_П, m_П, G_П-так называемые переменные параметры упругости:

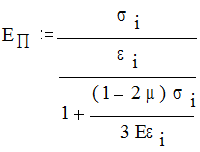                                                                                (2.2)                                                  

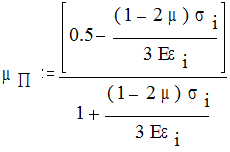
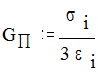
Как следует из формул (2.2), связь между “переменными параметрами” имеет тот же вид, что и для упруих постоянных E, G, m:

G_П=E_П/2(1+m) .

В частном случае для так называемого несжимаемого тела, у которого  m=1/2, по формулам (2.2)

E_П=3G_П=s_i/e_i  , m_P=1/2,

т.е. «переменный модуль упругости» совпадает c секущим модулем, а «переменный коэффициент поперечной деформации» равен половине.

  Для решения упруго-пластической задачи по методу переменных параметров упругости используется процесс последовательных приближений. В первом приближении принимается, что переменные параметры упругости равны параметрам упругости, и решается упругая  задача, в результате чего определяются напряжения и деформации первого приближения  s_x1 …, t_zx1 …, e_x1 …, g_zx1 … . По этим величинам в каждой точке тела при помощи формул  s_i=(1/2)^0.5((s_x-s_y)²+(s_y-s_z)²+(s_z-s_x)²+6(t²_xy+t²_yz+t²_zx))^0,5

      e_i =(2/9)^0,5((e_x-ey)²+(e_y-e_z)²+(e_z-e_x)²+(3\/2)(g²_xy+g²_yz+g²_zx))^0,5 

подсчитывают интенсивности напряжений и деформаций в первом приближении s_i1  и  e_i1.

 В координатах e_i, s_i (рис.(  )) напряженное и деформированное состояние некоторой точки тела изображается точкой 1, лежащей на луче, тангенс угла которого пропорционален величине 3G. Она принимается равной отношению интенсивности напряжений s_i1^П, соответвующей интенсивности деформаций e_i1^П по диаграмме деформирования (рис(  )):

3G=s_i1^П/e_i1.

  По величинам  s_i1^П, e_i1^П определяют параметры E^П₁ и m^П₁. Эти величины будут различными в разных точках тела. Таким образом, возникает задача определения напряжений в «неоднородном» теле, параметры  упругости в различных точках которого различны. Далее решают  эту задачу, определяют напряжения и деформации  s_x2 …, t_zx2 …, e_x2 …, g_zx2 …, являющиеся вторым приближением. По этим величинам в каждой точке тела при помощи формул s_i=(1/2)^0.5((s_x-s_y)²+(s_y-s_z)²+(s_z-s_x)²+6(t²_xy+t²_yz+t²_zx))^0,5

e_i =(2/9)^0,5((e_x-ey)²+(e_y-e_z)²+(e_z-e_x)²+(3\/2)(g²_xy+g²_yz+g²_zx))^0,5 

подсчитывают интенсиывности напряжений и деформаций во втором приближении   s_i2, e_i2.

   В координатах  e_i, s_i напряженное и деформированное состояния некоторой точки тела изображаются точкой 2 (рис.(  )), лежащей на луче, тангенс угла которого пропорционален величине 3G₁^П.

  В третьем приближении величину 3G принимают равной отношению интенсивности напряжений s_i2^П, соответствующей интенсивности деформаций e_i2 по диаграмме деформирования

3G₂^П=s_i2^П/e_i2.

Далее процесс повторяется до тех пор, пока результаты в некотором приближении не будут близки к соответствующим результатам в предыдущем приближении. Обычно это имеет место уже для третьего приближения. Таким образом, практика расчетов показывает, что процесс всегда является сходящимся, причем скорость сходимости процесса значительна.