Сети и системы радиосвязи и средства их информационной защиты: Методические указания к лабораторным работам, страница 10

9.  Объясните, как свойства гауссовского канала связи используются при моделировании процессов кодирования и декодирования.

10.   Опишите принцип блочного кодирования и декодирования, вид матрицы генератора систематического блочного кода, а также вид проверочной матрицы.

11.   Объясните особенности циклических кодов как разновидности блочных кодов.

Для подготовки ответов на вопросы использовать литературные источники [1], [2].

ЛАБОРАТОРНАЯ РАБОТА № 4

Исследование сверточного кодирования и декодирования

Цель работы: изучение наиболее распространенных видов сверточного помехоустойчивого кодирования и декодирования, использующихся в современных сетях и системах радиосвязи, вероятностей ошибок декодирования в различных условиях работы цифровых систем связи.

Лабораторная работа выполняется в среде Simulink, предназначенной для моделирования процессов, представленных в виде блок-схем, и входящей в состав пакета MatLab.

Обобщенная структура лабораторной работы представлена на рис.4.1.

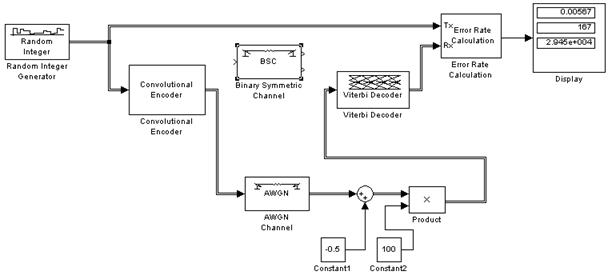
Рис. 4.1. Обобщенная структура лабораторной работы

Основным анализатором, используемым в работе, является анализатор вероятности ошибки декодирования ErrorRateCalculation.

Выполнение лабораторной работы

1. Для выполнения лабораторной работы необходимо запустить MatLab  и открыть в нем файл лабораторной работы с именем work_4.mdl. Ознакомиться с составом экспериментального стенда, сравнить с рис. 4.1.

2. Исследовать помехоустойчивость сверточных кодов для симметричного двоичного канала.

Так как закодированное сообщение должно передаваться за то же время, что и исходное, то это приводит к необходимости пересчета отношения сигнал-шум аналогично лабораторной работе №3: на графиках необходимо указывать значение , а при формировании модели канала использовать , применив формулу (3.1) и данные таблицы 3.1.

В работе используется сверточный кодер двоичных данных ConvolutionEncoder, свойства которого задаются полиномом , с параметрами:

-  длина кодового ограничения,

 - кодовые векторы, часто задаваемые в восьмеричной форме.

Примеры набора параметров для сверточных кодеров приведены в таблице 4.1 [3].

Таблица 4.1

Скорость кодирования	Длина кодового ограничения	Кодовые векторы
1 /2	3	5	7
	4	15	17
	5	23	35
	6	53	75
	7	133	171
1/3	3	5	7	7
	4	13	15	17
	5	25	33	37
	6	47	53	75
	7	133	145	175
1 /4	3	5	7	7	7
	4	13	15	15	15
	5	25	33	33	33
	6	53	53	53	53
	7	135	145	145	145
1/5	3	7	7	7	5	5
	4	17	17	13	15	15
	5	37	27	33	25	35
	6	75	71	73	65	57
	7	175	131	135	135	147

Экспериментально получить значения вероятностей ошибки декодирования для сверточных кодов со скоростью кодирования  1/2, 1/3, 1/4, 1/5. Длина кодового ограничения  выбирается в зависимости от номера бригады:

Таблица 4.2

Номер бригады	1	2	3	4	5
	3	4	5	6	7