Волновые явления на границе раздела двух сред

             10 ВОЛНОВЫЕ ЯВЛЕНИЯ НА ГРАНИЦЕ РАЗДЕЛА ДВУХ СРЕД

             Макроскопические параметры среды () могут изменятся скачком, образуя границу раздела двух сред. Эл.м. волна, проходя через границу раздела сред изменяет свои параметры, в общем случае все, кроме частоты. На границе должны выполняться граничные условия и закон сохранения энергии. На основании этих законов получается закон отражения и преломления на границе.

             Из множества границ раздела рассмотрим плоскую бесконечно протяженную границу. В прямоугольной системе координат границу раздела совмещают с одной из координатных плоскостей. Для удобства рассмотрения вводится нормальный  и касательный  орт-векторы к границе. Рисунок 10.1. Плоскостью падения эл.м. волны называют плоскость содержащую вектор Пойнтинга падающей волны и нормаль (плоскость М).

             По отношению к плоскости падения вектор  падающей эл.м. волны может быть ориентирован под любым углом. Выделяют нормальную поляризацию, когда  ориентирован по нормали к плоскости падения , и параллельную , когда вектор  находится в плоскости падения. Анализ производится раздельно для и .

             10.1 Законы отражения и преломления

             На основании граничных условий получают законы отражения и преломления. Они выполняются на любой границе в любой ее точке, в общем виде запишутся они так:

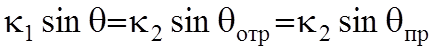                                       ,                              (10.1)

             где 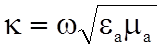 - волновое число,

                     - угол падения,

                     - угол отражения,

                    - угол преломления.

             Рисунок 10.2. Приравнивая в (10.1) первые члены равенства получаем закон отражения, а вторые – закон преломления:

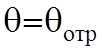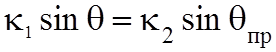                                       ;   .                                  (10.2)

             Причем векторы  и  лежат в плоскости падения. Закон преломления можно записать в следующем виде:

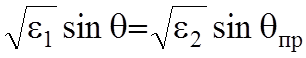                                       ;                                             (10.2 а)

                                       ;   ,

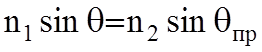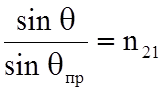             где - коэффициент преломления среды, - относительный коэффициент преломления.

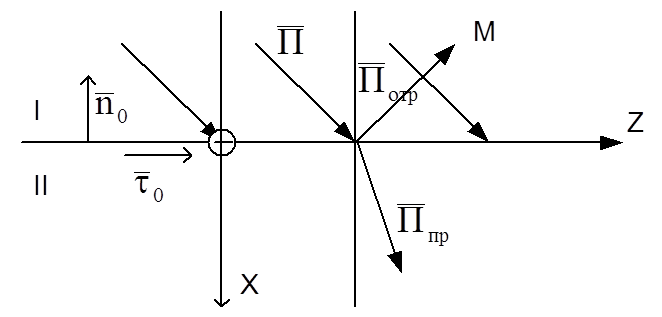             Рисунок 10.1

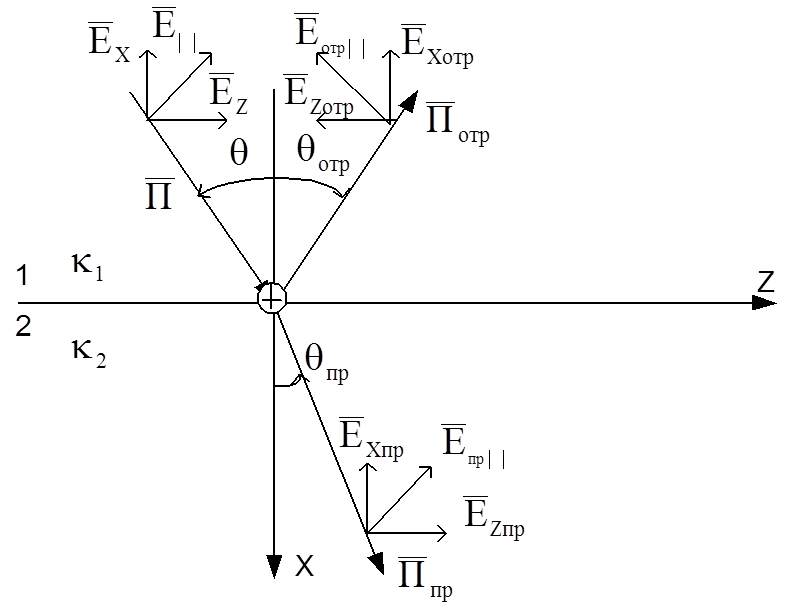Рисунок 10.2

             В (10.2 а) , и они сократились.

             Параметры среды обычно известны, поэтому зная один из углов по (10.2), рассчитывают другой угол.

             Если , то , то есть угол преломления . Если , то . При этом угол преломления может быть близок или равен p/2. Угол падения , при котором =p/2 называют критическим . При всех падения существует отраженная и преломленные волны, они являются однородными плоскими. При углах падения и уже не существует преломленной волны, она можно сказать переходит в первую среду, где совместно с отраженной волной образуется более сложная эл.м. волна. Комплекс явлений происходящих при этом,  называют полным внутренним отражением. Законы отражения и преломления одинаковы для нормальной и параллельной поляризации, поэтому они справедливы и для произвольной поляризации.

             10.2 Коэффициенты отражения и прохождения

             Для расчета амплитуды и фаз отраженной и преломленной волн вводятся эти коэффициенты:

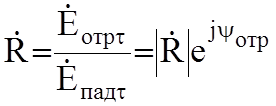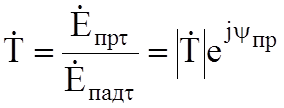                                       ;   ,        (10.3)

где  - комплексная амплитуда отраженной волны, касательная составляющая к границе.

Коэффициенты вводятся через отношение комплексных амплитуд касательных к границе отраженной волны к падающей, преломленной к падающей.

 - коэффициент отражения, - угол потери фазы при отражении, - коэффициент прохождения, - его фаза.

Коэффициенты зависят от параметров сред и углов  и  следующим образом:

             ;   ;

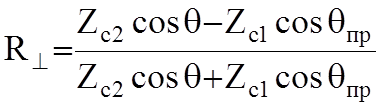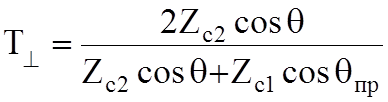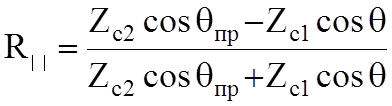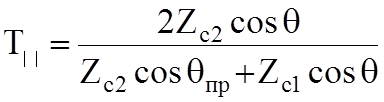             ;       (10.4)

             10.3 Нормальное падение. Полное прохождение

При нормальном падении на границу двух диэлектриков q=0 и согласно (10.2) угол преломления =0, тогда из (10.4) получаем:

                                        ; .

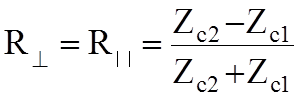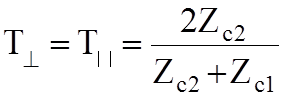Отраженная эл.м. волна будет отсутствовать R=0, если  , а Т=1, то есть при согласовании сред. Этот случай имеет место и в линиях передачи нагруженных на входное сопротивление антенны, приемника и т.д. Условием полного согласования является равенство волнового сопротивления линии Z_Л и нагрузки Z_Н.

При угле падения q¹0 коэффициент отражения =0 только при , то есть отсутствие границы раздела, а =0 при  и при , где - угол падения, при котором отсутствует отраженная волна, его называют углом Брюстера. Если падающая волна произвольно поляризована, то при угле падения равном углу Брюстера отраженная волна будет поляризована только нормально плоскости падения.