8 ОДНОРОДНЫЕ ПЛОСКИЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В
ИЗОТРОПНОЙ СРЕДЕ
Однородной
волной называют волну, в которой фазовый фронт совпадает с амплитудным фронтом,
или точнее амплитуда вектора ![]() (и вектора
(и вектора ![]() ) имеет одно и тоже значение амплитуды и
одно и тоже направление в каждой точке волновой поверхности. Так как векторы
поля одинаковы в каждой точке, то они вообще не зависят от координат этой
поверхности. Поэтому однородная плоская волна характеризуется соотношениями:
) имеет одно и тоже значение амплитуды и
одно и тоже направление в каждой точке волновой поверхности. Так как векторы
поля одинаковы в каждой точке, то они вообще не зависят от координат этой
поверхности. Поэтому однородная плоская волна характеризуется соотношениями:
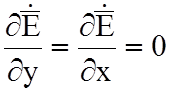 ;
; 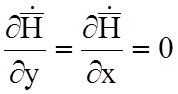
Если
эл.м. волна распространяется по оси Z, то векторы поля зависят только
от координаты «Z», и не зависят от «X» и «Y», и
нет проекций векторов поля на ось «Z». Такую волну называют еще
поперечной и обозначают «Т» – волной. Рассмотрим распространение эл.м. волны в
реальной среде с параметрами ![]() . Под действием вектора
. Под действием вектора
![]() распространяющейся плоской волны в среде с
s¹0 наводятся токи проводимости с плотностью
распространяющейся плоской волны в среде с
s¹0 наводятся токи проводимости с плотностью ![]() , на
поддержание которых нужно затрачивать энергию. Поэтому амплитуды векторов поля
при распространении в такой среде уменьшаются. Это так называемые тепловые
потери, среда нагревается. Закон уменьшения амплитуд – экспоненциальный,
учитывается множителем
, на
поддержание которых нужно затрачивать энергию. Поэтому амплитуды векторов поля
при распространении в такой среде уменьшаются. Это так называемые тепловые
потери, среда нагревается. Закон уменьшения амплитуд – экспоненциальный,
учитывается множителем ![]() , если эл.м. волна
распространяется по оси Z.
, если эл.м. волна
распространяется по оси Z.
В общем случае эл. магнитную волну, распространяющуюся по оси «Z» можно записать так:
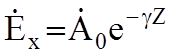 ;
; 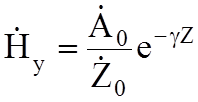 ,
,
где
![]() - амплитуда вектора
- амплитуда вектора ![]() ,
,
![]() - волновое сопротивление
среды,
- волновое сопротивление
среды,
g - коэффициент распространения, равный:
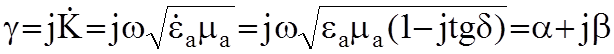 ,
,
где
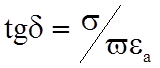 - тангенс угла диэлектрических потерь.
- тангенс угла диэлектрических потерь.
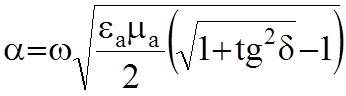 - коэффициент затухания,
- коэффициент затухания, ![]() .
.
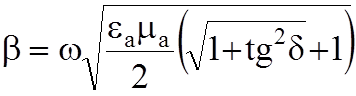 - коэффициент фазы,
- коэффициент фазы, ![]() .
.
Комплексные амплитуды поля запишутся так:
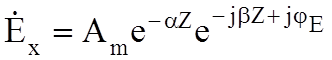 ;
; 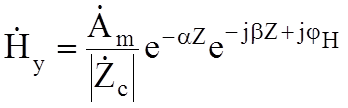 ,
,
где
![]() - начальная фаза векторов
- начальная фаза векторов ![]() и
и ![]() .
.
Мгновенные значения векторов поля:
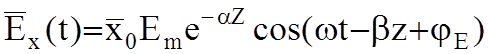 ;
;
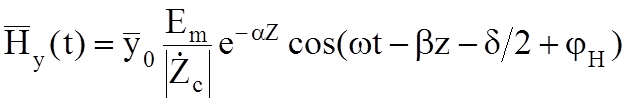 (8.1)
(8.1)
Это есть уравнение плоской эл.м. волны (волна «Т») в среде с проводимостью s¹0.
Волновое сопротивление среды с s¹0 есть величина комплексная:
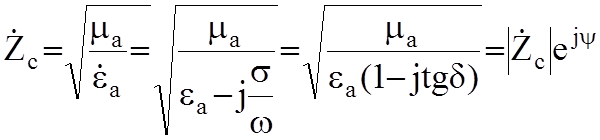 , (8.2)
, (8.2)
где
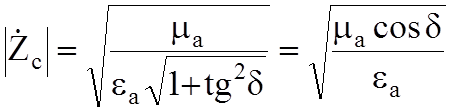 ,
,
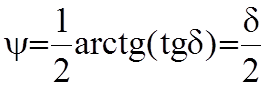 (8.3)
(8.3)
Таким
образом, в плоской эл.м. волне в среде с s¹0 (8.1) амплитуды векторов ![]() и
и ![]() уменьшаются на пути распространения по
экспоненциальному закону. Коэффициент затухания зависит от свойств среды (
уменьшаются на пути распространения по
экспоненциальному закону. Коэффициент затухания зависит от свойств среды (![]() ) и частоты w.
) и частоты w.
Фазы
векторов поля ![]() и
и ![]() сдвинуты
на угол
сдвинуты
на угол 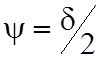 . При увеличении s в интервале 0£ s£¥, угол d изменяется от 0£ d £p/2, а 0£ y £p/4. Волновое сопротивление
. При увеличении s в интервале 0£ s£¥, угол d изменяется от 0£ d £p/2, а 0£ y £p/4. Волновое сопротивление 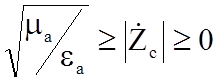 , с увеличением s проводимости среды стремится к нулю. На рисунке 8.1 изображена
структура поля волны в среде с проводимостью. С течением времени эл.м. волна
перемещается в направлении возрастающих значений Z со скоростью
, с увеличением s проводимости среды стремится к нулю. На рисунке 8.1 изображена
структура поля волны в среде с проводимостью. С течением времени эл.м. волна
перемещается в направлении возрастающих значений Z со скоростью 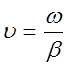 , векторы
, векторы ![]() и
и ![]() ограничены по амплитуде «неподвижными»
экспонентами
ограничены по амплитуде «неподвижными»
экспонентами ![]() .
.
Мгновенное
значение вектора Пойтинга имеет только одну составляющую ![]() , однако из-за существования в среде с
потерями сдвига по фазе
, однако из-за существования в среде с
потерями сдвига по фазе 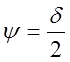 между векторами
между векторами ![]() и
и ![]() эта
составляющая принимает положительные и отрицательные значения. Это означает,
что в фиксированной точке наблюдения Z=const в течение
части периода Т энергия движется в направлении распространения волны (
эта
составляющая принимает положительные и отрицательные значения. Это означает,
что в фиксированной точке наблюдения Z=const в течение
части периода Т энергия движется в направлении распространения волны (![]() >0), а в течение другой – в
противоположном направлении (
>0), а в течение другой – в
противоположном направлении (![]() <0).
<0).
Среднее за период значение вектора Пойнтинга равно:
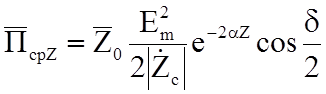 (8.4)
(8.4)
Поскольку
0£![]() £
£![]() , то cos
, то cos![]() >0, и следовательно
>0, и следовательно ![]() . Это означает, что в среднем эл.м. волна
переносит энергию в направлении распространения.
. Это означает, что в среднем эл.м. волна
переносит энергию в направлении распространения.
Средние за период значения объемных плотностей энергий электрического поля и магнитного поля равны:
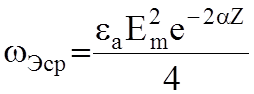 ;
; 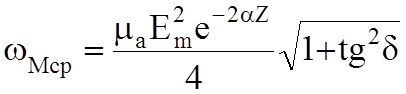 .
.
В
среде с потерями ![]() , с увеличением s отношение
, с увеличением s отношение 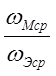 возрастает.
возрастает.
Скорость
переноса энергии 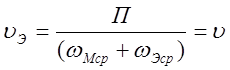 равна фазовой скорости
равна фазовой скорости 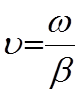 . Коэффициент фазы b зависит от частоты, отсюда и фазовая скорость u тоже зависит от частоты. Это явление называют дисперсией. Если с
ростом частоты фазовая скорость уменьшается – это нормальная дисперсия, если
увеличивается – это аномальная. В среде с потерями существует аномальная
дисперсия.
. Коэффициент фазы b зависит от частоты, отсюда и фазовая скорость u тоже зависит от частоты. Это явление называют дисперсией. Если с
ростом частоты фазовая скорость уменьшается – это нормальная дисперсия, если
увеличивается – это аномальная. В среде с потерями существует аномальная
дисперсия.
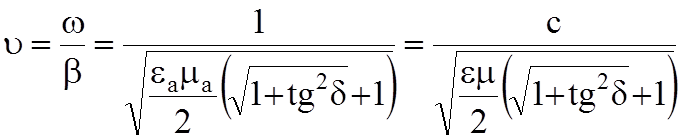 . (8.5)
. (8.5)
Длина волны в среде с проводимостью:
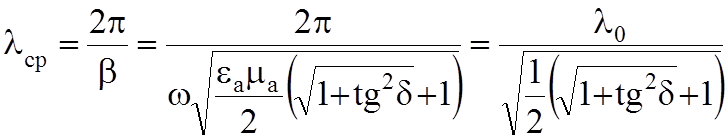 , (8.6)
, (8.6)
где
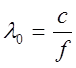 - длина волны в вакууме.
- длина волны в вакууме.
Таким образом фазовая скорость и длина волны в среде уменьшаются, а частота остается неизменной, т.е.:
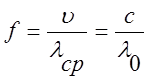
Затухание
амплитуд, происходящее при прохождении волной пути ![]() ,
характеризуется отношением:
,
характеризуется отношением:
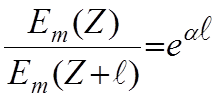 .
.
Выразим
затухание в децибелах (дБ) на пути ![]() ,
,
![]() , дБ. (8.7)
, дБ. (8.7)
Затухание на единице длины пути равно:
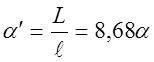 , дБ/м.
, дБ/м.
Амплитуда
вектора ![]() уменьшится в е=2,718 раз при прохождении
пути
уменьшится в е=2,718 раз при прохождении
пути 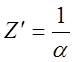 . Это расстояние называют «глубиной»
проникновения поля в среду, обозначают
. Это расстояние называют «глубиной»
проникновения поля в среду, обозначают ![]() . При
прохождении расстояния в несколько d амплитуды поля настолько
уменьшаются, что дальше волна практически не проникает. При больших a «глубина» проникновения d составит очень малые величины и поле будет
сосредоточено на поверхности такой среды (например металла). Это явление
называют поверхностным эффектом.
. При
прохождении расстояния в несколько d амплитуды поля настолько
уменьшаются, что дальше волна практически не проникает. При больших a «глубина» проникновения d составит очень малые величины и поле будет
сосредоточено на поверхности такой среды (например металла). Это явление
называют поверхностным эффектом.
В
реальном диэлектрике ![]() формулы могут быть упрощены:
формулы могут быть упрощены:
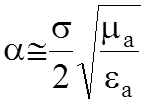 ;
; 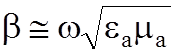 ;
; 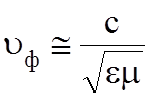 ;
;
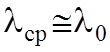 ;
; 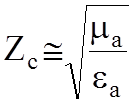 .
(8.8)
.
(8.8)
При
![]() :
:
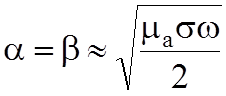 ;
; 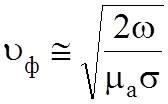 ;
;
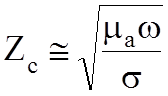 ;
; 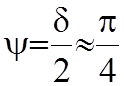 .
.
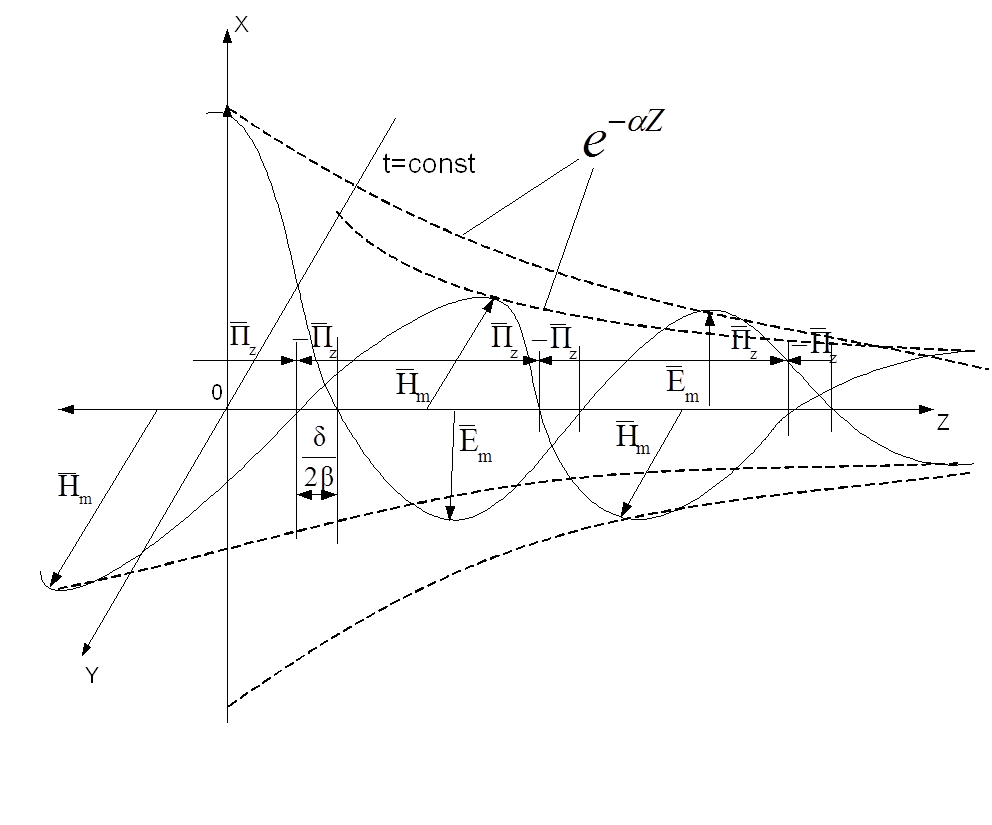
Рисунок 8.1
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.