Волновые явления на границе раздела двух сред, страница 3

             Рассмотрим случай идеального проводника и диэлектрика. Внутри идеального проводника поле равно нулю, , а коэффициенты отражения . Физически это означает, что касательные составляющие вектора  на границе проводника падающей волны и отраженной волны равны по величине и противоположны по направлению. Значения говорит  о том, что фаза отраженной волны вектора  меняется на обратную, а амплитуда не изменяется, так как 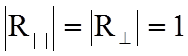. Таким образом, от идеального проводника происходит полное отражение не зависимо от угла падения q. В диэлектрике при этом формируется направляемая волна, как сумма падающей и отраженной волны. Все отмеченные выше свойства для направляемой волны, существующей в первой среде, присущи и результирующей волне при отражении от идеально проводящей поверхности. При отражении от реальной металлической поверхности в диэлектрике формируется также направляемая волна с теми же свойствами, а внутри металла поверхностной волны нет, а есть преломленная волна распространяющаяся под =0 с резко

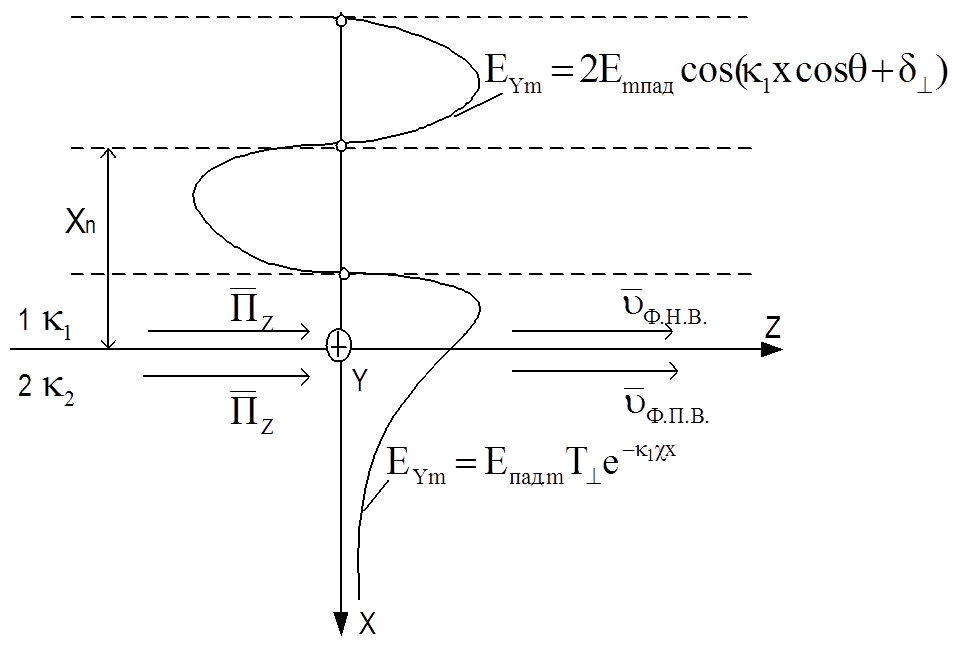             Рисунок 10.3

убывающей амплитудой по оси «X». Коэффициент затухания очень велик, поэтому поле сосредоточено в очень тонком слое у поверхности металла и очень мало по величине. Поэтому им можно пренебречь и считать, что существует полное отражение. Из свойств направляемой волны следует, что существует бесчисленное множество плоскостей, параллельных границе раздела на которых касательные составляющие , равны нулю и нормальная составляющая вектора . Такие же граничные условия выполняются на границе с металлической поверхностью, поэтому в этих сечениях «X_n» можно разместить параллельные друг другу металлические поверхности и между ними будет распространяться эл.м. волна. Это уже будет направляющая система, а если еще ограничить с боков, то получим прямоугольный волновод. Таким образом, в ограниченном металлическими стенами объеме может при определенных условиях существовать эл.м. поле.

             10.5 Падение эл.м. волны на границу диэлектрика и среды с потерями

             В этом случае плоская однородная эл.м. волна распространяется в диэлектрике с параметрами  и падает под углом q на плоскую поверхность раздела со второй средой с параметрами .

             В этом случае  является комплексной величиной:

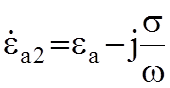                                       ,  а так же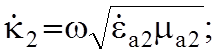         

                                       .

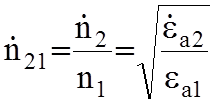             Из закона преломления 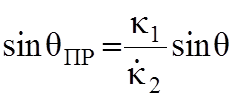 следует, что параметр нельзя рассматривать как геометрический угол, определяющий направление распространения преломленной волны. Из анализа поля следует, что преломленная волна является плоской и распространяется пол углом - истинный угол преломления, который равен:

                                       .

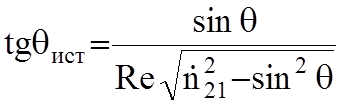             Амплитуда преломленной волны уменьшается по закону , то есть определяется  пройденным расстоянием в поглощающей среде, где - коэффициент затухания. Поверхности одинаковых амплитуд представляют собой плоскости x=const, параллельные границе раздела. Поверхности одинаковых фаз j=const перпендикулярны направлению распространения преломленной волны, таким образом, амплитудный и фазовый фронты пересекаются под углом .

             При q¹0 в среде с потерями () распространяется плоская неоднородная эл.м. волна. Рисунок 10.4.

             При q=0  амплитудный и фазовый фронты совпадают и волна становится однородной плоской. Если велико, то преломленная волна распространяется по нормали к поверхности =0. Для такой волны, плоской однородной, справедлива связь между параметрами  и  через волновое сопротивление среды:

                                       ,

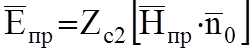которое выполняется и на границе. Граничные условия на любой границе выглядят так, . Подставляем их и получим:

                                                                                                   (10.8)

Это есть приближенные граничные условия Леонтовича-Щукина, которые связывают между собой касательные составляющие векторов поля в одной и той же среде на границе через характеристическое сопротивление второй среды Z_c2, называемое поверхностным импедансом.

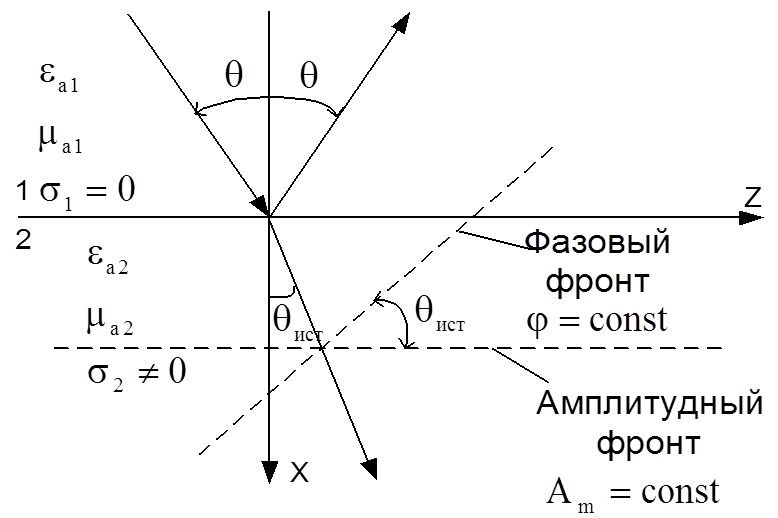             Рисунок 10.4