10.4 Полное внутреннее отражение
На
границе двух диэлектриков (s=0) при условии ![]() ,
, ![]() и
и ![]() происходит полное внутреннее отражение, то
есть нет преломленной волны. При этом из закона преломления:
происходит полное внутреннее отражение, то
есть нет преломленной волны. При этом из закона преломления:
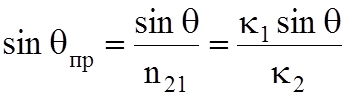
вытекает
неравенство ![]() , которое удовлетворяется лишь при
комплексном угле преломления
, которое удовлетворяется лишь при
комплексном угле преломления 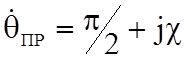 :
:
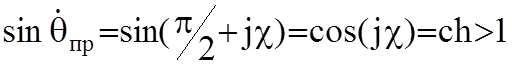 .
.
При
этом 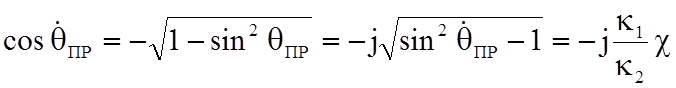 ,
,
где
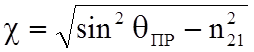 .
.
При
полном отражении модули коэффициентов отражения равны единице: (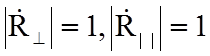 )
)
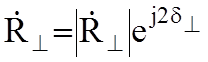 ,
, 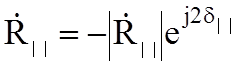 ,
,
где 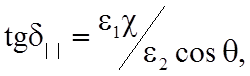
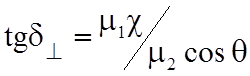 . (10.5)
. (10.5)
В
первой среде (![]() ) при полном отражении
формируется неоднородная плоская волна, распространяющаяся по оси Z.
Для параллельной поляризации вектор
) при полном отражении
формируется неоднородная плоская волна, распространяющаяся по оси Z.
Для параллельной поляризации вектор ![]() имеет нормальную и
касательную составляющие, а вектор
имеет нормальную и
касательную составляющие, а вектор ![]() только касательную:
только касательную:
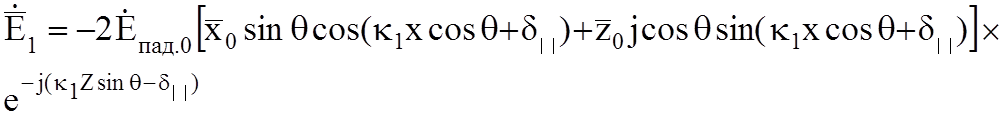
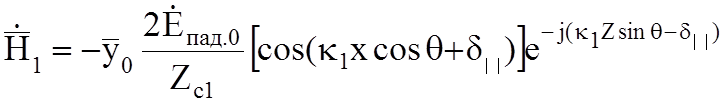 (10.6а)
(10.6а)
При нормальной поляризации падающей волны поле в первой среде:
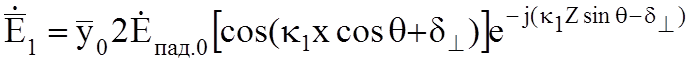 (10.6б)
(10.6б)
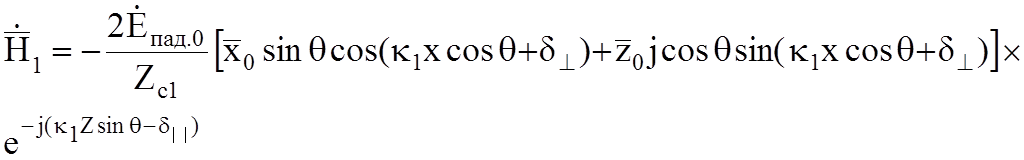 Перечислим свойства эл.м.
волны в первой среде при полном отражении:
Перечислим свойства эл.м.
волны в первой среде при полном отражении:
-
Эл.м. волна распространяется по оси «Z», о чем говорит фазовый
множитель ![]() .
.
-
Перенос энергии происходит только
по оси «Z». Вектор Пойнтинга определяют ![]() и
и
![]() при параллельной поляризации, и
при параллельной поляризации, и ![]() и
и ![]() - для
нормальной. Эти составляющие находятся в фазе и создают вектор Пойнтинга,
направленный по оси «Z», то есть
- для
нормальной. Эти составляющие находятся в фазе и создают вектор Пойнтинга,
направленный по оси «Z», то есть ![]() . Вдоль оси «X»
переноса энергии нет, так как составляющие
. Вдоль оси «X»
переноса энергии нет, так как составляющие ![]() и
и ![]() ,
, ![]() и
и ![]() сдвинуты на угол p/2 (
сдвинуты на угол p/2 (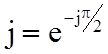 ). Поэтому такую волну называют
направляемой, а границу раздела направляющей поверхностью (или системой).
). Поэтому такую волну называют
направляемой, а границу раздела направляющей поверхностью (или системой).
- Фазовый фронт волны, характеризуемый уравнением:
![]()
определяет плоскую волну, волновые поверхности которой, описываются уравнением Z=const, ориентирован параллельно плоскости XOY. Поверхности равных амплитуд определяются X=const, параллельны границе раздела. Таким образом поверхности равных амплитуд и равных фаз взаимно перпендикулярны. Такую волну называют неоднородной волной.
-
В направляемой волне имеются
продольные составляющие векторов поля (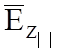 и
и 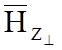 ), это значит, что волна перестала быть
плоской, и стала поперечно-продольной (класса «Е» или класса «Н»).
), это значит, что волна перестала быть
плоской, и стала поперечно-продольной (класса «Е» или класса «Н»).
- Фазовая скорость определяется общим уравнением:
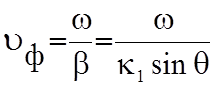 ;
;
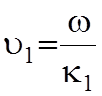 - фазовая скорость
плоской эл.м. волны в среде с параметрами первой среды. Как видно
- фазовая скорость
плоской эл.м. волны в среде с параметрами первой среды. Как видно ![]() , и направляемая волна является ускоренной.
, и направляемая волна является ускоренной.
- Длина волны направляемой равна:
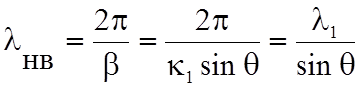 ,
,
где
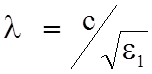 - длина волны в первой среде, не
ограниченной.
- длина волны в первой среде, не
ограниченной.
Как
видно ![]() .
.
-
Существует множество плоскостей,
параллельных границе раздела, на которых тангенциальная составляющая ![]() и нормальная
и нормальная![]() равны
нулю. Расстояния Xn от
границы раздела определяются уравнениями:
равны
нулю. Расстояния Xn от
границы раздела определяются уравнениями:
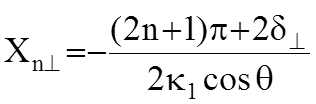 ;
; 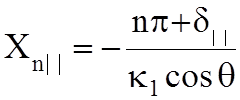 ,
,
n=(0, 1, 2, 3…)
-
Энергия переносится только по оси
«Z» вдоль границы со скоростью![]() ,
и она меньше скорости u1 в данной
среде. Среднее значение вектора Пойнтинга
,
и она меньше скорости u1 в данной
среде. Среднее значение вектора Пойнтинга ![]() имеет
только одну продольную составляющую:
имеет
только одну продольную составляющую:
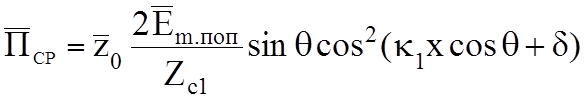 .
.
-
В поперечном направлении устанавливается
стоячая волна, происходит колебательный процесс, энергия в среднем не
переносится и ![]() по «X» равен нулю.
по «X» равен нулю.
Рассмотрим эл.м. поле во второй среде. Уравнения поля:
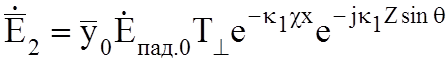
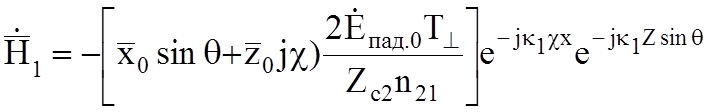 (10.7а)
(10.7а)
для нормально поляризованных волн и:
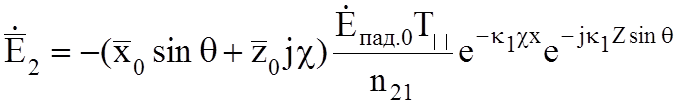
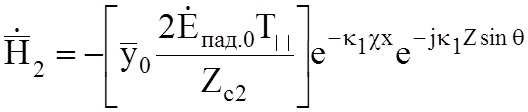 (10.7б)
(10.7б)
для параллельно поляризованных волн.
Из
уравнений поля следует, что во второй среде свойства те же, что и в первой
среде. Отличия состоит в том, что амплитуда бегущих волн по оси «Z»
убывает по оси «X» по экспоненциальному закону (![]() )
и фазовая скорость волн меньше таковой в данной среде. Такую волну называют
поверхностной замедленной, она как бы прилипает к границе раздела, с удалением
от границы ее амплитуда резко уменьшается. Заметим, что фазовые скорости
направляемой волны в первой среде и во второй среде для поверхностной волны,
одинаковые. Скорость распространения энергии во второй среде такая же как и в
первой, т.е.
)
и фазовая скорость волн меньше таковой в данной среде. Такую волну называют
поверхностной замедленной, она как бы прилипает к границе раздела, с удалением
от границы ее амплитуда резко уменьшается. Заметим, что фазовые скорости
направляемой волны в первой среде и во второй среде для поверхностной волны,
одинаковые. Скорость распространения энергии во второй среде такая же как и в
первой, т.е. ![]() .
.
Таким образом, при полном отражении в оптически менее плотной среде вдоль границы раздела распространяется поперечно-продольная замедленная волна с экспоненциально убывающими амплитудами по мере удаления от границы. Перенос энергии также вдоль границы (Рисунок 10.3).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.