Сутність економічної безпеки підприємства. Сутність системи економічної безпеки підприємства. Основні типи та характеристика негативного впливу на економічну безпеку підприємства. Методи оцінки ризиків, страница 19

Незалежно від виду матриці гри потрібно вибрати таку стратегію гравця, що була б найбільш вигідною у порівнянні з іншими.

Невизначеність, пов'язану з відсутністю інформації про ймовірності стану середовища, називають «безнадійною». У таких випадках, а саме їх ми й будемо розглядати, для визначення найкращих рішень використовуються критерії Лапласа, Севіджа, Гурвіца, Вальда.

При виборі оптимального рішення недоцільно зупинятися на виборі одного з критеріїв, тому що в ряді випадків це може привести до невиправданих результатів при виборі рішення, що веде до значних втрат будь-якого змісту. Тому має сенс застосовувати кілька критеріїв у сукупності.

Застосування різних критеріїв для різних завдань вибору оптимального рішення в умовах невизначеності показує, що підхід, який базується на комплексному застосуванні зазначених критеріїв, може стати визначальним.

Дані, необхідні для ухвалення рішення, задаються у вигляді матриці, рядки якої відповідають можливим методам керування ризиком, а стовпці - можливим станам середовища. Таких станів два: у випадку прояву негативного боку ризику або у випадку відсутності втрат від ризику.

Кожному методу й можливому стану середовища відповідає результат, що визначає втрати підприємства при виборі даного методу керування і реалізації даного стану середовища.

Критерій Лапласа припускає, якщо немає достатніх підстав вважати, що ймовірність того або іншого рішення має нерівномірний розподіл, то вони приймаються однаковими. Тоді завдання зводиться до пошуку найбільш оптимального варіанта, який в свою чергу - до пошуку як максимального значення (якщо мова йде про прибуток), так і мінімального (якщо мова йде про втрати).

Вихідне завдання можна розглядати як завдання ухвалення рішення в умовах невизначеності, коли вибирається дія, що дає найменші втрати.

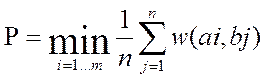                                ,                                 (3.1)

де P - оптимальне рішення;

1/n - імовірність реалізації стану;

W (a_i,b_j) – оптимальна стратегія при даних значеннях;

a_i – дія при мінімальних втратах;

b_j - дія при максимальних втратах.

Критерій Вальда (мінімакс) є найбільш обережним, оскільки він ґрунтується на виборі найкращої з найгірших можливостей. Тобто для кожного рішення вибирається гірша ситуація (максимальні втрати) і серед них відшукується та, яка принесе максимальний ефект (краща з гірших).

                                           M = MIN MAX w(b_i, a_i).                    (3.2)

Критерій Севіджа. Полягає - у досягненні мінімального ризику. При виборі стратегії за цим методом необхідно скласти матрицю втрат. Елементи цієї матриці відбивають збитки від помилкової дії або вигоду, упущену в результаті ухвалення певного рішення у відповідному стані. Розрахунок елементів нової матриці виконується за формулою:

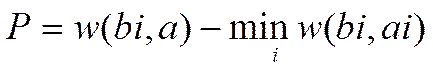                              .                        (3.3) 

Критерій Гурвіца встановлює баланс між випадками
 крайнього оптимізму та крайнього песимізму зважуванням обох способів
 поводження з відповідними вагами α і (1- α), де 0 ≤ α ≤ 1. Якщо
 обрана стратегія представляє втрати або витрати, критерій вибирає дія, при якій отриманий результат розраховується за формулою:

          .            (3.4)

Параметр α визначається як показник оптимізму:

-  при α = 1 критерій занадто оптимістичний;

-  при α = 0 він занадто песимістичний.

-  значення α між 0 і 1 може визначатися залежно від схильності особи, що приймає рішення, до песимізму або оптимізму. При відсутності яскраво вираженої схильності α = 1/2 представляється найбільш розумним.

Даний  підхід з розробки моделі керування ризиками на підприємстві, а також варіант кінцевого вибору критеріїв вибору оптимального рішення з мінімізації ризиків на підприємстві дозволяє значно спростити процес керування ризиком.

Після того як за яким не будь з методів потенційний ризик оцінено, визначається рівень так званого прийнятного ризику - прийнятний у випадку виникнення яких-небудь проблем рівень збитку або недоодержання прибутку.