Завдання та методичні вказівки до контрольної роботи з курсу «Статистика», страница 4

Варіант 8

Таблиця 14 – Розподіл фермерських господарств району за

                       розміром угідь

Господарства за розміром угідь, га	До 30	30-40	40-50	50-60	60 і більше	Разом
Кількість господарств	10	20	12	10	8	60

Визначити середній розмір фермерських угідь.

Варіант 9

Таблиця 15 – Розподіл співпрацівників  за рівнем

                       середньомісячної заробітної плати

Заробітна плата, грн	До 300	300-350	350-400	400-450	450-500	500 і більше	Разом
Кількість співпрацівників, чол.	20	90	140	120	80	50	500

Визначити середній розмір заробітної плати співпрацівників.

Варіант 10

Таблиця 16 – Розподіл населення по забезпеченості житловою

                        площею

Розмір житлової площі на одного члена сім’ї, м2	До 10	10-12	12-14	14-16	16-18	18-20	20 і більше	Разом
Кількість сімей, %	30	23	25	9	6	4	3	100

Визначити середній розмір загальної житлової площі, що приходиться на одного члена сім’ї.

За нижченаведеними даними визначити:

1) середню величину ознаки, що аналізується звичайним шляхом і способом моментів;

2) моду і медіану;

3) побудувати графіки.

Методичні вказівки до виконання задачі 2

Середні величини відносяться до узагальнюючих показників і найбільш широко використовуються в економіко-статистичному аналізі.

Середніми величинами в статистиці називають показники, які дають узагальнену характеристику ознаки одиниць однорідної сукупності, яка варіює.

У статистиці розрізняють середні степеневі і середні описового характеру. Середні степеневі вираховуються як прості, так і зважені.

Середні степеневі можна виразити такими формулами:

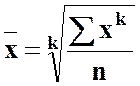   -  проста;  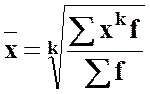    -  зважена.         (4)

Якщо k = 1, отримують середню арифметичну:

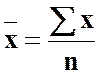   -  проста;  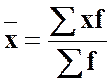    -  зважена.                    (5)

Розрахунок середньої способом моментів базується на важливих властивостях середньої арифметичної, а саме:

‑ якщо всі варіанти збільшити або зменшити на деяке постійне число А, то середня також збільшиться або зменшиться на це ж саме число

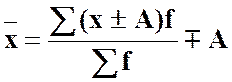;                                      (6)

‑  якщо всі варіанти збільшити або зменшити в d разів, то середня також збільшиться або зменшиться в стільки ж разів:

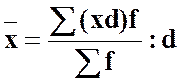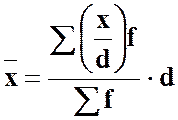  ;    ;                     (7)

‑  якщо всі частоти збільшити або зменшити в d разів, то середня від цього не зміниться:

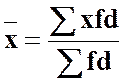  ;    .                              (8)

Виходячи з цього можна розраховувати умовну середню, так званий умовний момент першого порядку

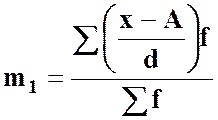  ,                                        (9)

тоді середня способом моментів буде розраховуватись за формулою

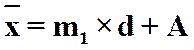                                              (10)

До середніх описового характеру відносять моду і медіану.

Мода (Мо) – значення ознаки, яке зустрічається частіше за все, тобто варіант, якому відповідає найбільша частота.

Для інтервального ряду мода вираховується за формулою

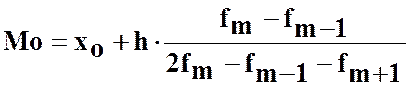,                                       (11)

де  – нижня межа модального інтервалу;

     h – величина модального інтервалу;

      – частота модального інтервалу;

      – частота інтервалу, попереднього модальному;

      – частота інтервалу, який іде за модальним.

Медіана (Ме) – варіант, який розділяє ряд розподілу умовно кількісно навпіл за сумою частот.

Для інтервального ряду медіана розраховується за формулою:

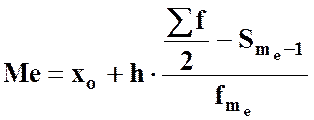  ,                                       (12)

Де  – нижня межа медіанного інтервалу;

      h – величина медіанного інтервалу;

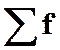       – сума частот ряду;

       – накопичена частота інтервалу, попереднього медіанному;

      - частота медіанного інтервалу.

Розрахунок середньої наведено в таблиці 17