Расчет системы автоматической стабилизации заданного значения выходной координаты, страница 7

>0, что свидетельствует о том, что скорректированная система является устойчивой.

5.3 Оценка качества переходного процесса

На основе (5.5) можно записать операторное уравнение:

                                                                  (5.11)

Пусть , тогда на основе (5.11) можно записать уравнение в символической форме:

,                                       (5.12)

где

     

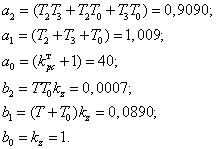
На основе (2) можно записать:

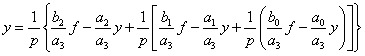.                         (5.13)

В соответствии с методом последовательного интегрирования, уравнению (5.13) соответствует следующая система дифференциальных уравнений в форме Коши:

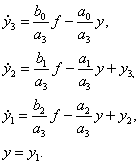                                                                                   (5.14)

Пусть для решения системы уравнений (5.14) используется метод Эйлера, в котором

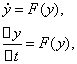
где - шаг интегрирования.

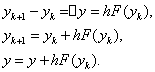
На основе (5.14) окончательно можно записать:

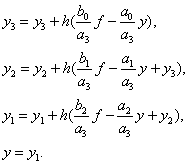                                                                                  (5.15)

Переходный процесс по возмущающему воздействию в скорректированной системе представлен на рисунке.

На основе рисунка можно определить следующие значения показателей качества переходного процесса:

1.  Время регулирования – 1,115 c.

2.  Величина перерегулирования .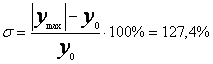

3.  Вид переходного процесса – колебательный.

4.  Частота собственных колебаний – f_k = 3,47.

5.  Период собственных колебаний –T_k = 0,288.

6.  Количество колебаний – 4.

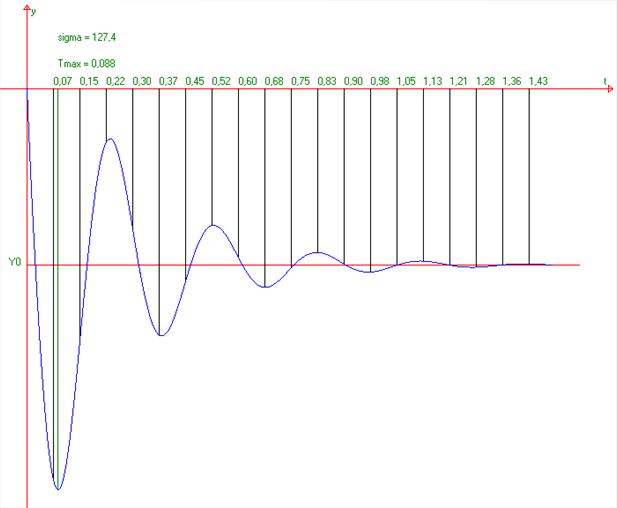
Рисунок 5.4 – Переходный процесс скорректированной системы.

Приложение А

uses crt, graph;

const      path = 'C:\bp\bgi';

                mash = 220;

var

                T,T0,T2,T3,dx1,Tre,Tmax,Per,tr,sigma,a0,a1,a2,a3,b0,b1,b2,tt,h,tpr,y, y1, y2, y3,pr,ymax,ymax1:real;

                i,j,Krs,z,Kz,gd,gm:integer;

                zn1,zn2,zn3:boolean;

                mast, masy, maspr:array[1..1500] of real;

                f: text;

procedure Initab;

begin

                a3:=T0*T2*T3;     a2:=T0*T2 + T0*T3 + T2*T3;

                a1:=T0 + T2 + T3;     a0:=Krs + 1;

                b2:=Kz*T*T0;     b1:=Kz*(T0 + T);

                b0:=Kz;     h:=a1/(10*a0);

                tt:=0;pr:=0;

end;

function newY:real;

begin

                pr:=b2/a3*z - a2/a3*y + y2;

                y2:=y2 + h*(b1/a3*z - a1/a3*y + y3);

                y3:=y3 + h*(b0/a3*z - a0/a3*y);

                y1:=y1 + h*pr;

                newY:=y1;

end;

procedure grafik;

var          zz: integer;

                st: string;

begin

                gd:= detect;

                initgraph(gd, gm, path);

                settextstyle(2, horizdir, 0);

                str(sigma:3:1,st);

                st:='S='+st+'%';