Экономика и менеджмент \ Основы теории управления

Расчет системы автоматической стабилизации заданного значения выходной координаты, страница 6

где      ;

                                                                                                  (5.2)

Структурная схема скорректированной системы приведена на рисунке 5.2.

В соответствии с теорией управления можно принять:

                                                                                                  (5.3)

Пусть , тогда, учитывая (5.3) и (5.2)  получим:

 мОм;

 мкФ;

 мкФ.

Пусть . Тогда передаточная функция скорректированной системы по управляющему воздействию с учетом (5.3) имеет вид:

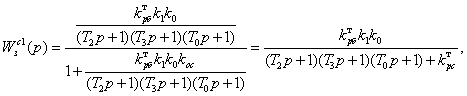             (5.4)

где      .

Пусть . Тогда передаточная функция скорректированной системы по возмущающему воздействию имеет вид:

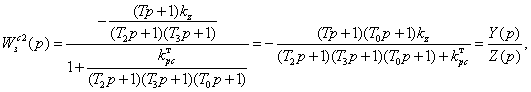        (5.5)

Используя принцип суперпозиции, учитывая (5.5) и (5.4), можно записать изображение выходного сигнала скорректированной системы:

.                                                                    (5.6)

5.2 Анализ устойчивости скорректированной системы

5.2.1 Устойчивость системы по критерию Гурвица

Поскольку устойчивость системы не зависит от вида входного сигнала, то положим . Тогда анализ устойчивости можно проводить на основе структурной схемы, представленной на рисунке 5.3.

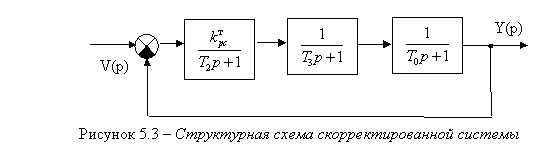
Передаточная функция в замкнутом состоянии:

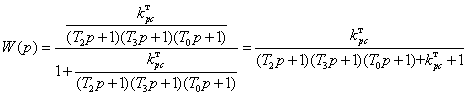            (5.7)

Приравняв знаменатель к нулю, запишем характеристическое уравнение:

                        ,                          (5.8)

где

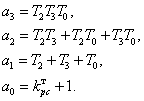                                                                                  (5.9)

С учетом исходных данных можно рассчитать коэффициенты характеристического уравнения скорректированной системы в замкнутом состоянии.

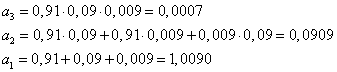
                                                                                 (5.10)

На основе (4.6) рассчитаем граничное значение передаточного коэффициента разомкнутой системы:

Так как , то скорректированная система является устойчивой.

5.2.2 Устойчивость системы по критерию Найквиста

Для определения устойчивости скорректированной системы необходимо также построить логарифмические частотные характеристики звеньев системы.

, дБ.

;

;

;

, дБ

На рисунке 5.4 представлено логарифмическая частотная характеристика разомкнутой системы. На основе формулы (4.7)  и рисунка (5.4) определим запас устойчивости по фазе:

Скачать файл