Расчет системы автоматической стабилизации заданного значения выходной координаты, страница 5

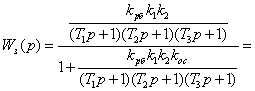
                      (4.1)

Приравняв знаменатель к нулю, получим характеристическое уравнение.

                        ,                           (4.2)

где

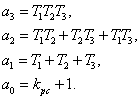                                                                                   (4.3)

С учетом исходных данных можно рассчитать коэффициенты характеристического уравнения исходной системы в замкнутом состоянии.

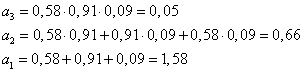
                                                                           (4.4)

Для характеристического уравнения системы в замкнутом состоянии (4.2) можно записать главный определитель Гурвица третьего порядка:

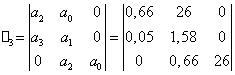
Система является устойчивой, если при  все определители Гурвица являются положительными:

                                     (4.5)

Так как определитель Гурвица второго порядка меньше нуля, то система в исходном состоянии является неустойчивой.

На основе (4.5) и с учетом (4.3) можно записать граничное значение передаточного коэффициента системы в разомкнутом состоянии:

.                                                                (4.6)

Подставив значения постоянных времени, можно найти искомую величину:

.

Система является неустойчивой, так как .

4.2 Устойчивость по критерию Найквиста

Условием применения критерия является необходимость приведения исходной структурной схемы к одноконтурной. При этом следует учитывать соотношение между постоянными времени (). Преобразованная структурная схема приведена на рисунке 4.2.

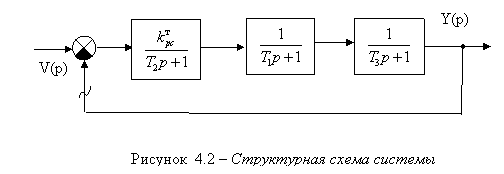
Для определения устойчивости системы необходимо построить логарифмические частотные характеристики звеньев системы.

, дБ.

;

;

;

, дБ

На рисунке 4.3 представлена логарифмическая частотная характеристика разомкнутой системы. Запас устойчивости по фазе определяется по формуле:

.                                                                                    (4.7)

Используя рисунок 4.3 и формулу (4.7), найдем запас устойчивости по фазе:

<0, что свидетельствует о том, что система является неустойчивой.

5 Коррекция динамических свойств системы

Поскольку исходная система при заданных параметрах является неустойчивой, то необходима коррекция динамических свойств системы.

5.1 Расчет параметров корректирующего устройства

Схема решающего блока, выполняющего функции коррекции динамических свойств системы приведена на рисунке 5.1.

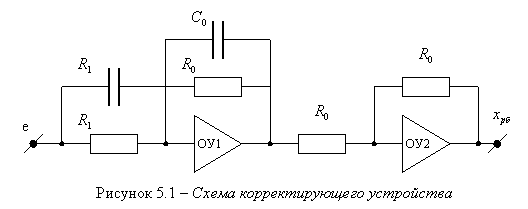
Схема описывается следующей передаточной функцией:

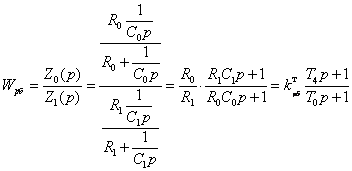,                             (5.1)