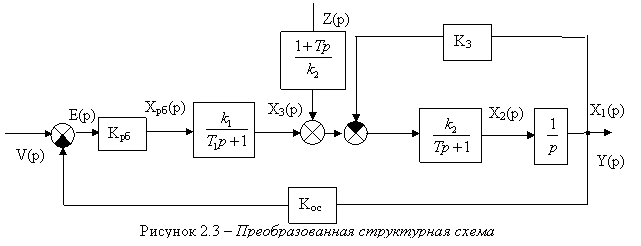
При ![]() передаточная функция ОУ по
управляющему сигналу
передаточная функция ОУ по
управляющему сигналу ![]() равна:
равна:
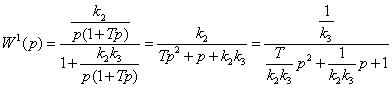 (2.3)
(2.3)
Приравнивая знаменатель передаточной функции (2.3) к нулю, можно записать общее характеристическое уравнение ОУ:
![]() (2.4)
(2.4)
Исходя из исходных данных, можно записать:
![]()
![]() (2.5)
(2.5)
Найдем дискриминант уравнения (2.5):
![]() (2.6)
(2.6)
Исходя из (2.6), уравнение (2.5) имеет действительные корни, таким образом, ОУ может быть представлен последовательным соединением двух пропорциональных инерционных звеньев I-го порядка. Структурная схема ОУ по управляющему воздействию представлена на рисунке 2.4.
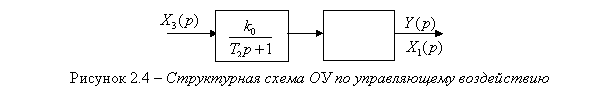
![]() (2.7)
(2.7)
Уравнения (2.3) и (2.7) должны соответствовать, то есть на их основе можно записать следующую систему уравнений:
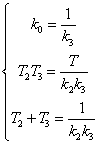 (2.8)
(2.8)
На основе (2.8) и с учетом исходных данных, можно записать:
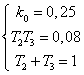 (2.9)
(2.9)
Таким образом, окончательно объект управления имеет следующие параметры:
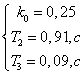
На основе рисунка 2.4 можно записать:
![]() (2.10)
(2.10)
На основе (2.1) и (2.2) при ![]() можно записать
передаточную функцию объекта управления:
можно записать
передаточную функцию объекта управления:
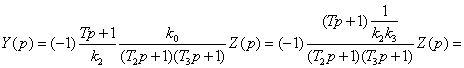
![]() , (2.11)
, (2.11)
где ![]() .
.
С учетом принципа суперпозиции на основе (2.10) и (2.11) окончательно можно записать изображение выходного сигнала:
![]() (2.12)
(2.12)
Таким образом, окончательная структурная схема исходной системы представлена на рисунке 2.5.
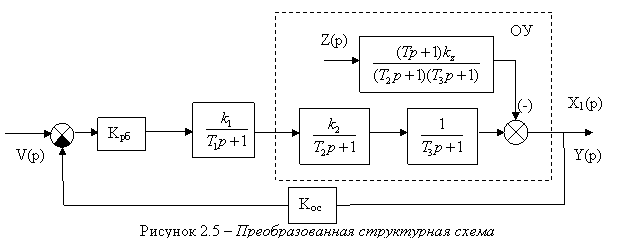
При ![]() на основе рисунка 2.5 можно записать
передаточную функцию исходной системы по управляющему воздействию
на основе рисунка 2.5 можно записать
передаточную функцию исходной системы по управляющему воздействию
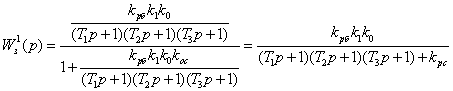 , (2.13)
, (2.13)
где ![]() - передаточный коэффициент
разомкнутой системы.
- передаточный коэффициент
разомкнутой системы.
На основе (2.13) можно записать изображение выходной системы:
![]() (2.14)
(2.14)
При ![]() передаточная функция исходной
системы по возмущающему воздействию имеет вид:
передаточная функция исходной
системы по возмущающему воздействию имеет вид:
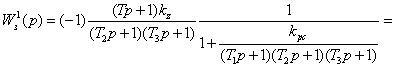
![]() (2.15)
(2.15)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.