Расчет системы автоматической стабилизации заданного значения выходной координаты, страница 4

                                                    (2.16)

С учетом принципа суперпозиции на основе формул (2.14) и (2.16) можно записать окончательно изображение выходного сигнала исходной схемы:

. (2.17)

3 Статический расчет

Пусть . Значит, рассмотрим исходную разомкнутую систему без обратной связи. Используя теорему о предельном значении, на основе (2.17) можно записать в установившемся режиме уравнение статики.

,          (3.1)

где       - заданное значение выходной координаты разомкнутой системы;

                - величина, на которую уменьшается выходная координата                                                      разомкнутой системы при действии возмущения.

Пусть и , а (максимальное возмущающее воздействие, исходя из исходных данных). Следовательно,

Поскольку выполняется условие ,                                          (3.2)

где       - требуемая точность стабилизации системы в статическом режиме (из                                  исходных данных),

то разомкнутая система должна быть заменена замкнутой системой автоматической стабилизации заданного значения выходной координаты.

На основе (2.17) можно записать уравнение статики замкнутой системы (ЗС):

                                   ,                          (3.3)

где       - заданное значение выходной координаты ЗС;

            - величина, на которую уменьшается выходная координата ЗС при                                          действии возмущения.

Поскольку задание на проектирование предполагает выполнение в замкнутой системе условия вида

                                   ,                          (3.4)

то, используя знак равенства в (3.4), окончательно можно записать расчетную формулу требуемого значения передаточного коэффициента разомкнутой системы:

                          .                (3.5)

Поскольку , то расчет требуемого передаточного коэффициента РБ проводится по формуле

                                               .               (3.6)

4 Анализ устойчивости системы

Устойчивость – это свойство системы возвращаться в прежнее состояние равновесия после вывода ее из этого состояния и прекращения действия возмущения.

4.1 Устойчивость по критерию Гурвица

Устойчивость системы зависит от ее структуры и значений параметров элементов. Если система устойчива, то при любом воздействии переходные процессы затухающие, то есть устойчивость не зависит от входных сигналов. Положим, что , и соответствующая этому условию схема представлена на рисунке 4.1.

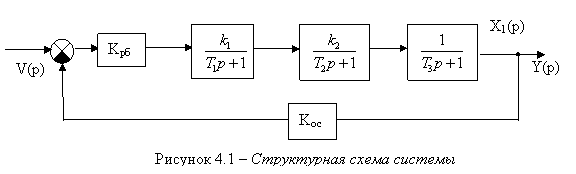
Передаточная функция системы в замкнутом состоянии имеет вид