Решение нелинейных алгебраических уравнений аналитическим, табличным и графическим способами, а также методом деления отрезка пополам

Министерство образования  Российской Федерации

Новосибирский Государственный Архитектурно-строительный 

Университет Сибстрин)

Кафедра прикладной математики

Отчет по лабораторной работе №1

Вариант №5

Выполнил студент

                                                                                           321 группы

                                                                                                       Гербер Ю.А.    

                                                                                          Проверила

                                                                                                    Федорченко И.А.

Новосибирск 2010

Часть 1 : Решение нелинейных алгебраических уравнений (НАУ)

Формулировка задания:

1.  Исследовать заданное уравнение на наличие корней аналитически, таблично и графически (с помощью графопостроителя). Найти интервалы изоляции всех корней уравнения. Выписать интервалы изоляций для каждого корня.

2.  Для каждого интервала изоляции [a;b] с заданной точностью ε=0,001 найти корни уравнения с использованием метода деления отрезка пополам и метода Ньютона. Результаты занести в Таблицу 1:

Метод	№ корня	Интервал изоляции	Значение корня	Количество итераций

3.  Для одного из корней проследить изменение количества итераций, необходимых для решения уравнения с точностью ε=0,01; ε=0,001; ε=0,0001. Результаты занести в    Таблицу 2

№ корня	Точность	Значение корня	Количество итераций

4.  Повторить задание пункта 2, использовав один из методов 3-7 (по указанию преподавателя). Для этого метода составить Таблицы 3,4, аналогичные Таблицам 1 и 2. Сравнить все методы по количеству итераций (скорости сходимости).

Решение

Дано     F(x)=0,5^x +2-(x-1)² =0

1.  аналитический способ:

F(x)=0,5^x +2-(x-1)² =0

  1)поведение функии на

   F(-∞)=+∞ >0;  F(+∞)=-∞ <0

2)производная

F’(x)= 0,5^x Ln(0,5) -2(x-1)

2. табличный способ

х	F(x)
-6	17
-5,5	5,004833996
-5	-2
-4,5	-5,622583002
-4	-7
-3,5	-6,936291501
-3	-6
-2,5	-4,593145751
-2	-3
-1,5	-1,421572875
-1	0
-0,5	1,164213562
0	2
0,5	2,457106781
1	2,5
1,5	2,103553391
2	1,25
2,5	-0,073223305
3	-1,875
3,5	-4,161611652
4	-6,9375
4,5	-10,20580583
5	-13,96875

3. графический способ

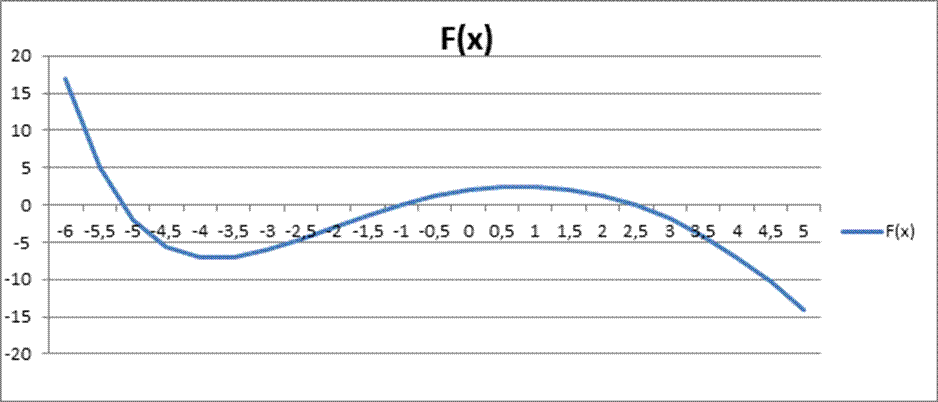
Из  табличного и  графического способов  видно что функция имеет 3 корня . Интервалы изоляции корней

[-6;-5]-               1-й интервал

[-3;-0,5]-            2-й интервал          

[1;3]-                 3-й интервал

4.Метод деления отрезка пополам 

Суть метода: Проверяем интервал F(a)*F(b)<0. Определяем середину интервала 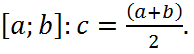 Проверяем, какому из двух отрезков (a; c) или (b; c) принадлежит искомый корень, т.е. f(a)*f(c)<0, тогда b=c, либо f(c)*f(b)<0, тогда a=c. Концы нового отрезка, которому принадлежит корень, обозначаем a, b и повторяем процедуру до тех пор, пока не будет достигнуто условие сходимости итерационного процесса: |b-a|<ε.

Метод  деления отрезка пополам, интервал1 [-6;-5]
N	a	b	c	f(a)	f(b)	f(с)	pogr
0	-6	-5	-5,5	17,00	-2	5,004833996	1
1	-5,5	-5	-5,25	5,004833996	-2	0,99212768	0,5
2	-5,25	-5	-5,125	0,99212768	-2	-0,619377555	0,25
3	-5,25	-5,125	-5,1875	0,99212768	-0,619377	0,156080062	0,125
4	-5,1875	-5,125	-5,15625	0,156080062	-0,619377	-0,239038299	0,0625
5	-5,1875	-5,15625	-5,171875	0,156080062	-0,239038	-0,04334922	0,03125
6	-5,1875	-5,17188	-5,1796875	0,156080062	-0,043349	0,05589503	0,015625
7	-5,17969	-5,17188	-5,17578125	0,05589503	-0,043349	0,006155666	0,0078125
8	-5,17578	-5,17188	-5,173828125	0,006155666	-0,043349	-0,018626042	0,00390625
9	-5,17578	-5,17383	-5,174804688	0,006155666	-0,018626	-0,00624251	0,001953125
10	-5,17578	-5,1748	-5,175292969	0,006155666	-0,0062425	-4,52528E-05	0,000976563