Математика \ Численные методы

Решение нелинейных алгебраических уравнений аналитическим, табличным и графическим способами, а также методом деления отрезка пополам, страница 5

Метод Якоби
i	x1	x2	x3	x4	pogr
0	0	0	0	0
1	-0,185185	0	0,2380952	0,285714	0,285714
2	0,044092	0,24641	0,4038801	0,31746	0,24641
3	0,138229	0,271269	0,2684495	0,101559	0,215902
4	-0,019082	0,102203	0,1547017	0,079777	0,169066
5	-0,083671	0,085147	0,2476229	0,227911	0,148134
6	0,024263	0,201146	0,3256673	0,242856	0,115999
7	0,068578	0,212848	0,2619124	0,141218	0,101637
8	-0,005477	0,133259	0,2083648	0,130965	0,079589
9	-0,035883	0,12523	0,2521081	0,2007	0,069735
10	0,014928	0,179837	0,2888481	0,207735	0,054607
11	0,03579	0,185347	0,258835	0,159889	0,047846
12	0,000928	0,147879	0,2336271	0,155061	0,037467
13	-0,013386	0,1441	0,2542196	0,18789	0,032828
14	0,010533	0,169806	0,2715152	0,191202	0,025707
15	0,020354	0,1724	0,2573863	0,168678	0,022524
16	0,003943	0,154762	0,2455195	0,166405	0,017638
17	-0,002796	0,152982	0,2552136	0,181859	0,015454
18	0,008465	0,165084	0,2633556	0,183419	0,012102
19	0,013088	0,166305	0,2567043	0,172815	0,010603
20	0,005362	0,158002	0,251118	0,171745	0,008303
21	0,00219	0,157164	0,2556815	0,179021	0,007275
22	0,007491	0,162861	0,2595144	0,179755	0,005697
23	0,009667	0,163436	0,2563833	0,174763	0,004992
24	0,00603	0,159527	0,2537535	0,174259	0,003909
25	0,004537	0,159133	0,2559018	0,177684	0,003425
26	0,007032	0,161815	0,2577062	0,17803	0,002682
27	0,008057	0,162085	0,2562322	0,17568	0,00235
28	0,006345	0,160245	0,2549941	0,175443	0,00184
29	0,005642	0,16006	0,2560055	0,177055	0,001612
30	0,006817	0,161322	0,2568549	0,177218	0,001263
31	0,007299	0,161449	0,256161	0,176112	0,001106
32	0,006493	0,160583	0,2555782	0,176	0,000866

1.1. 3. Метод Гаусса-Зейделя с точностью ε=0.001. Метод заключается в:

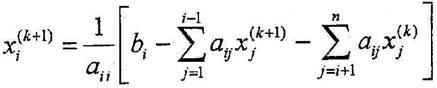
Где k – номер итерации, n – количество уравнений, x_i⁽⁰⁾ – начальное приближение

Гауса-Зейделя
i	x1	x2	x3	x4	pogr
0	0	0	0	0
1	-0,18519	0,026455	0,3023432	0,29554	0,3023
2	0,071527	0,2306486	0,2544442	0,125092	0,2567
3	-0,01467	0,1341588	0,253439	0,195317	0,0965
4	0,013324	0,1700489	0,2576373	0,170174	0,0359
5	0,004587	0,1579293	0,2554702	0,178507	0,0121
6	0,007228	0,1617977	0,2563208	0,175879	0,0039
7	0,00645	0,1606096	0,2560241	0,176679	0,0012
8	0,006674	0,1609641	0,2561209	0,176442	0,0004

Вывод: при решении системы линейных алгебраических уравнений тремя методами ,т все корни получились примерно одинаковые. Но самым удобным и точным являеться метод обратной матрицы. Из приближенных методов наиболее удобным и менее емким является метод Гаусса-Зейбеля (8 итераций) , в то время как метод простой итерации(Якоби) требует намного больше шагов итераций(32)

1 2 3 4 5

Скачать файл