Математика \ Численные методы

Решение нелинейных алгебраических уравнений аналитическим, табличным и графическим способами, а также методом деления отрезка пополам, страница 4

метод релаксации, интервал 1[-6;-5]
k	x	\|Xk+1 -Xk\|	F(Xk)
0	-5,5	0	5,004833996
1	-5,253104532	0,246895468	1,035289229
2	-5,202032265	0,051072267	0,344959601
3	-5,185014925	0,01701734	0,124109864
4	-5,178892412	0,006122513	0,04575191
5	-5,176635406	0,002257006	0,017011816
6	-5,175796189	0,000839217	0,006345445
7	-5,17548316	0,00031303	0,002369637
8	-5,175366262	0,000116898	0,000885301
9	-5,175322589	4,36731E-05	0,000330804
10	-5,17530627	1,6319E-05	0,000123617

метод релаксациии, интервал 2 [-3;-0,5]
k	x	\|Xk+1 -Xk\|	F(Xk)
0	-1,75	0	-2,198914339
1	-0,912224631	0,837775369	0,225342175
2	-0,998078873	0,085854242	0,005019341
3	-0,999991217	0,001912344	2,29554E-05
4	-0,999999963	8,7459E-06	9,62513E-08


метод релаксациии, интервал 3 [1;3]
k	x	\|Xk+1 -Xk\|	F(Xk)
0	2	0	1,25
1	2,563924574	0,563924574	-0,276745202
2	2,439073838	0,124850736	0,113468484
3	2,490263971	0,051190133	-0,042912995
4	2,470904217	0,019359754	0,016818846
5	2,478491865	0,007587648	-0,006506317
6	2,475556608	0,002935258	0,002530014
7	2,476697997	0,00114139	-0,000981849
8	2,476255046	0,000442951	0,000381333
9	2,47642708	0,000172034	-0,000148058

Таблица 3

Метод	№ корня	Интервал изоляции	Значение корня	Количество итераций
релаксации	1	[-6;-5]	-5,175796189	6
	2	[-3; -0,5]	-0,999999963	4
	3	[1; 3]	2,476255046	8

Таблица 4

№ корня	Точность	Значение корня	Количество итераций
1	0,01	-5,178892412	4
	0,001	-5,17579618	6
	0,0001	-5,175322589	9

Вывод:

Сравнив результаты расчетов разных методов вычислений , не трудно заметить , что для нахождения корней уравнений , больше всего итераций надо для метода деления отрезка пополам(10-12),для метода Ньютона (2-7) и для метода релаксации (4-8). Быстрее всего сходяться методы Ньтона и релаксации.

Часть 2. Методы решения систем линейных алгебраических уравнений.

Решением системы линейных алгебраических уравнений , состоящей из N уравнений, является вектор , состоящий из N компонент, который при подстановки в исходную систему дает набор из N тождеств. Здесь А – матрица коэффициентов системы, - вектор неизвестных, - вектор правых частей. При решении небольших систем удобно использовать точные методы решения, к которым относятся метод обратной матрицы, метод Крамера, метод Гаусса и другие. При решении систем большой размерности, используют итерационные методы.

Формулировка задания

Найти решение системы линейных уравнений Ax̅=b̅, где

матрица А				b
27	-3	-8	-15	-5
3	21	-5	-12	0
8	5	21	-7	5
15	12	7	35	10

1. Метод обратной матрицы x̅ = A^-1b̅, используя функции Excel МУМНОЖ и МОБР.

Результаты вычислений:

матрица А^-1				вектор х
0,029	-0,004234	0,005977	0,0121634	0,006625
-0,01	0,040037	0,002301	0,0096829	0,160884
-0,01	-0,011147	0,040947	-0,000243	0,256098
-0,01	-0,009683	-0,01154	0,0200874	0,176495

2.Метод простой итерации с точностью ε=0.001. Метод простой итерации заключается в:

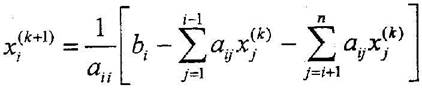
Где k – номер итерации, n – количество уравнений, x_i⁽⁰⁾ – начальное приближение.

1 2 3 4 5

Скачать файл