|
Метод деления отрезка пополам, интервал 2 [-3;-0,5] |
|||||||
|
N |
a |
b |
c |
f(a) |
f(b) |
f(с) |
pogr |
|
0 |
-3 |
-0,5 |
-1,75 |
- 6,00 |
1,164213562 |
-2,198914339 |
2,5 |
|
1 |
-1,75 |
-0,5 |
-1,125 |
-2,198914339 |
1,164213562 |
-0,334609535 |
1,25 |
|
2 |
-1,125 |
-0,5 |
-0,8125 |
-0,334609535 |
1,164213562 |
0,47109591 |
0,625 |
|
3 |
-1,125 |
-0,8125 |
-0,96875 |
-0,334609535 |
0,47109591 |
0,081167562 |
0,3125 |
|
4 |
-1,125 |
-0,96875 |
-1,046875 |
-0,334609535 |
0,081167562 |
-0,123647508 |
0,15625 |
|
5 |
-1,04688 |
-0,96875 |
-1,0078125 |
-0,123647508 |
0,081167562 |
-0,020451233 |
0,078125 |
|
6 |
-1,00781 |
-0,96875 |
-0,98828125 |
-0,020451233 |
0,081167562 |
0,030557836 |
0,0390625 |
|
7 |
-1,00781 |
-0,98828 |
-0,998046875 |
-0,020451233 |
0,030557836 |
0,005102911 |
0,01953125 |
|
8 |
-1,00781 |
-0,99805 |
-1,002929688 |
-0,020451233 |
0,005102911 |
-0,007661797 |
0,009765625 |
|
9 |
-1,00293 |
-0,99805 |
-1,000488281 |
-0,007661797 |
0,005102911 |
-0,001276347 |
0,004882813 |
|
10 |
-1,00049 |
-0,99805 |
-0,999267578 |
-0,001276347 |
0,005102911 |
0,001914056 |
0,002441406 |
|
11 |
-1,00049 |
-0,99927 |
-0,99987793 |
-0,001276347 |
0,001914056 |
0,000319048 |
0,001220703 |
|
12 |
-1,00049 |
-0,99988 |
-1,000183105 |
-0,001276347 |
0,000319048 |
-0,000478601 |
0,000610352 |
|
Метод деления отрезка пополам, интервал 3 [1;3] |
|||||||
|
N |
a |
b |
c |
f(a) |
f(b) |
f(с) |
pogr |
|
0 |
1 |
3 |
2 |
2,50 |
-1,875 |
1,25 |
2 |
|
1 |
2 |
3 |
2,5 |
1,25 |
-1,875 |
-0,073223305 |
1 |
|
2 |
2 |
2,5 |
2,25 |
1,25 |
-0,073223305 |
0,647724104 |
0,5 |
|
3 |
2,25 |
2,5 |
2,375 |
0,647724104 |
-0,073223305 |
0,302151353 |
0,25 |
|
4 |
2,375 |
2,5 |
2,4375 |
0,302151353 |
-0,073223305 |
0,118197018 |
0,125 |
|
5 |
2,4375 |
2,5 |
2,46875 |
0,118197018 |
-0,073223305 |
0,023421038 |
0,0625 |
|
6 |
2,46875 |
2,5 |
2,484375 |
0,023421038 |
-0,073223305 |
-0,024667473 |
0,03125 |
|
7 |
2,46875 |
2,484375 |
2,4765625 |
0,023421038 |
-0,024667473 |
-0,000564817 |
0,015625 |
|
8 |
2,46875 |
2,476563 |
2,47265625 |
0,023421038 |
-0,000564817 |
0,011442709 |
0,0078125 |
|
9 |
2,472656 |
2,476563 |
2,474609375 |
0,011442709 |
-0,000564817 |
0,005442596 |
0,00390625 |
|
10 |
2,474609 |
2,476563 |
2,475585938 |
0,005442596 |
-0,000564817 |
0,002439802 |
0,001953125 |
|
11 |
2,475586 |
2,476563 |
2,476074219 |
0,002439802 |
-0,000564817 |
0,000937721 |
0,000976563 |
5.Метод Ньютона
Суть метода: Выберем начальное приближение x0ϵ[a; b]. Следующие итерации
определяются по формуле 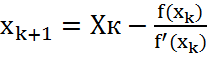
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.