Министерство образования Российской Федерации
Новосибирский Государственный Архитектурно- Строительный
Университет.
(СИБСТРИН).
Кафедра информационных
Систем и технологий.
Лабораторная работа 1.
«Решение нелинейных алгебраических уравнений»
Вариант 19
Выполнил:
Студент 324 группы
Назаров М.Г.
Проверила:
Руев Г.А.
Новосибирск 2010 г.
Описание методов решения.
1. Метод деления отрезка пополам. Определяем середину отрезка [а,b]: С = (а+b)/2 и проверяем, какому из двух отрезков (а,с) или (с,b) принадлежит искомый корень, т.е. проверяем: f(a)f(c)<0 либо f(c)f(b)<0. Концы нового отрезка, которому принадлежит корень, обозначаем а, bи повторяем процедуру до тех пор, пока не будет достигнуто условие сходимости итерационного процесса: |b-а|<ε. Вычисления оформляются в виде таблицы
|
а |
b |
с |
f(a) |
f(c) |
b-a |
|
0 |
|||||
|
1 |
|||||
|
. . . . |
где ао , bo - границы интервала изоляции корня; Сi = (ai+ bi)/2, i= 0,1,2...;
сi-1, если f(ai-1)f(сi-1) > 0; bi-1, если f(аi-1)f(сi-1) > 0; ai=bi=i= 1,2,3,.
ai-1, в противном случае сi-1, в противном случае
2. Метод простой итерации. Исходное уравнение приводится к виду, удобному для применения метода простой итерации: х = φ(х), где, например, φ(х) = х - с f(x). Параметр с подбирается таким образом, чтобы выполнялось достаточное условие сходимости метода:
|φ `(х)|<1для всех хє[а,b]. Начальное приближение x0= (а + b)/2. Следующие итерации
находим по формуле: xk+1=φ(xk). Часто с берут в виде:
с = 2/ (М + т), где М = mах(f `(х)), т = min(f '(x)). Вычисления оформляются в виде таблицы:
|
к |
X |
|Х к-1| |
|||
|
0 |
х0 |
||||
|
1 …. |
X1
…. |
|x1-х0| ……… |
|||
Условие окончания итерационного процесса |хк — xк-1|<ε
3. Метод Ньютона.
Итерации определяются по формуле ![]()
Вычисление оформить в виде таблицы:
|
к |
x |
f(x) |
f'(x) |
|xk — xk-1| |
|
0 1 ….. |
х0 x1 …… |
f(xo) f(x1) ….. |
f `(xo) f `(x1) …… |
|x1 — x0| ……. |
a, если f(a) f ``(a) > 0
где x0=
b, в противном случае
Условие окончания итерационного процесса |xk-xk-1|<ε
4. Метод хорд. Итерации определяются по формулам:
Если f(a) f"(a) > 0, то х0 =b хк+1=a-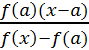
Если f(а)f"(а)<0, то хо=а
хк+1=хк-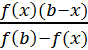
Вычисление оформить в виде таблицы:
|
к |
x |
f (x) |
| xк-xk-1| |
|
0 1 |
х0 X, |
f(xo) |
|x1 - х0| |
Условие окончания итерационного процесса |xk-xk-1|<ε
метод деления отрезков пополам
|
i |
a |
b |
c |
f(a) |
f© |
b-a |
|
0 |
1 |
2 |
1,5 |
-4 |
-2,375 |
1 |
|
1 |
1,5 |
2 |
1,75 |
-2,375 |
-0,95313 |
0,5 |
|
2 |
1,75 |
2 |
1,875 |
-0,95313 |
-0,04883 |
0,25 |
|
3 |
1,875 |
2 |
1,9375 |
-0,04883 |
0,456787 |
0,125 |
|
4 |
1,875 |
1,9375 |
1,90625 |
-0,04883 |
0,199371 |
0,0625 |
|
5 |
1,875 |
1,90625 |
1,890625 |
-0,04883 |
0,074131 |
0,03125 |
|
6 |
1,875 |
1,890625 |
1,882813 |
-0,04883 |
0,012368 |
0,015625 |
|
7 |
1,875 |
1,882813 |
1,878906 |
-0,04883 |
-0,0183 |
0,007813 |
|
8 |
1,878906 |
1,882813 |
1,880859 |
-0,0183 |
-0,00298 |
0,003906 |
|
9 |
1,880859 |
1,882813 |
1,881836 |
-0,00298 |
0,004687 |
0,001953 |
|
10 |
1,880859 |
1,881836 |
1,881348 |
-0,00298 |
0,00085 |
0,000977 |
Метод простой итерации Метод Ньютона
|
k |
x |
|xk-xk-1| |
|
0 |
1,5 |
|
|
1 |
1,931818 |
0,431818 |
|
2 |
1,857402 |
0,074416 |
|
3 |
1,890968 |
0,033566 |
|
4 |
1,876994 |
0,013973 |
|
5 |
1,883042 |
0,006047 |
|
6 |
1,880465 |
0,002577 |
|
7 |
1,88157 |
0,001105 |
|
8 |
1,881098 |
0,000473 |
|
Метод хорд
|
k |
x |
f(x) |
|xk-xk-1| |
|
0 |
1 |
-4 |
|
|
1 |
1,8 |
-0,608 |
0,8 |
|
2 |
1,875622 |
-0,04398 |
0,075622 |
|
3 |
1,880861 |
-0,00297 |
0,005239 |
|
4 |
1,881214 |
-0,0002 |
0,000353 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.