Тема. Точные методы решения СЛАУ (систем линейных алгебраических уравнений).
Рассмотрим СЛАУ
, где 
и
известны, 
, требуется найти 
.
Определение. Точными методами решения СЛАУ называются методы, которые в предположении отсутствия ошибок округлений позволяют найти точное решение системы за конечное число операций.
Как правило, в точных методах исходную систему уравнений эквивалентными преобразованиями приводят к системе с диагональной, треугольной или унитарной матрицей, решение которой легко находится. Либо исходную матрицу раскладывают на произведение двух матриц, тогда решение системы сводят к решению двух систем с матрицами специального вида: треугольных, треугольной и диагональной, треугольной и унитарной и т.д.
В данной работе требуется решить систему уравнений каким-либо точным методом и оценить погрешность решения. Оценить погрешность решения можно одним из следующих способов.
A. Выбираем
некоторый n-мерный вектор 
(например,
), вычисляем вектор 
и решаем одновременно две системы , 
.
Обычно
считают, что относительные погрешности полученных решений 
и 
этих
систем мало отличаются, т.е.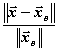 
и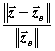 
имеют одинаковый порядок малости.
B. Вычисляем
вектор невязки 
. Тогда погрешность решения
находится из решения системы 
.
Здесь и далее приняты обозначения:
,
, 
,
, 
,
, 
,
, 
,
.
-
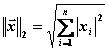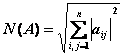спектральный радиус матрицы А – максимум модулей собственных
чисел этой матрицы.
1.
.
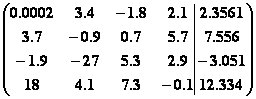2.
.
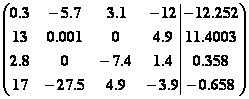3.
.
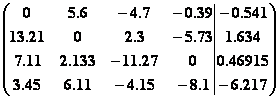4.
.
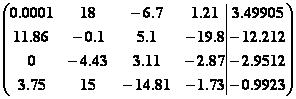5.
.
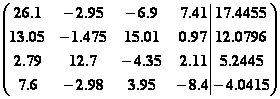6.
.
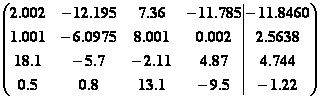7.
.
8.
.
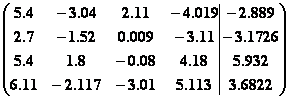9.
.
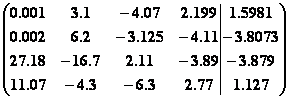10. 
.
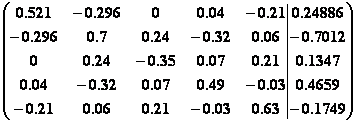11. 
.
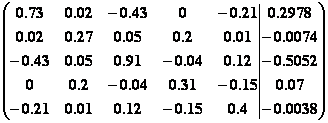Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
