Точные методы решения СЛАУ (систем линейных алгебраических уравнений), страница 2

12.  .

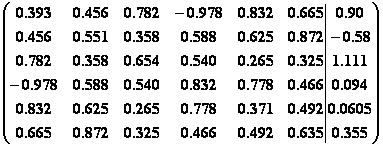13.  A  =  (a_ij),  ,  i,j  =  1,…,n.  Эта матрица А называется матрицей Гильберта.

Примечание. Выписаны расширенные матрицы. Последний столбец – это правая часть СЛАУ.

Варианты методов

1.  Схема единственного деления.

2.  Метод Гаусса с выбором главного элемента.

3.  Схема оптимального исключения.

4.  LU-разложение.

5.  Метод вращений.

6.  Метод квадратного корня.

7.  Метод Гаусса с выбором главного элемента по строке.

8.  Метод ортогонализации по строкам.

9.  Метод ортогонализации по столбцам.

10.  Метод отражений.

11.  Компактная схема Гаусса.

Задание

1.  Решить систему линейных уравнений точным методом. Вариант системы и выбор метода решения предварительно согласовать с преподавателем.

2.  Вывести на экран вычисленное решение,  вектор невязки.

3.  Оценить погрешность решения с помощью методов, изложенных ранее. Компоненты вектора  взять равными номеру фамилии студента в списке преподавателя. Выдать на экран оценку погрешности.

4.  Решить систему линейных уравнений для матрицы Гильберта (пример № 13), предварительно посчитав вектор . Посчитать вектор невязки. Порядок системы указывает преподаватель. На экран выдать точное решение , посчитанное решение  и вектор невязки .

Контрольные вопросы

1.  Дать определение точных методов решения СЛАУ. Изложить идеи построения точных методов.

2.  Знать алгоритм каждого метода решения СЛАУ.

3.  Знать достоинства и недостатки каждого метода.

4.  Для каких систем уравнений (свойства матрицы А) работают указанные методы?

5.  Какого числа операций при больших n требует каждый метод?

6.  Что является алгебраической основой схемы единственного деления метода исключения Гаусса (чему эквивалентна схема единственного деления)?

7.  Применим ли метод Гаусса с выбором главного элемента по строке, если все a_kk  =  0?

8.  Каковы общие недостатки точных методов?

9.  Как вычислить обратную матрицу с помощью точных методов решения СЛАУ?

10.  Как вычислить определитель, используя точные методы решения СЛАУ?

11.  Дана система линейных уравнений с трехдиагональной матрицей. Какой можно предложить метод решения? Почему?

12.  Для чего вычисляют вектор невязки?

13.  Как связаны между собой вектор невязки и вектор погрешности? Следует ли из малости вектора невязки малость вектора погрешности? (Под вектором погрешности понимаем  ).

14.  Доказать, что метод прогонки есть метод исключения Гаусса для решения системы уравнений с трехдиагональной матрицей.

15.  Вычислить и  для матрицы

.

16.  Пусть , где  – вектор-столбец. Показать, что А – ортогональная матрица и .