- время регулирования tP=0,5 c;
- перерегулирование σ=25%.
По заданным времени регулирования и регулированию определяется по монограмме Солодовникова, рисунок 7, частота среза системы.
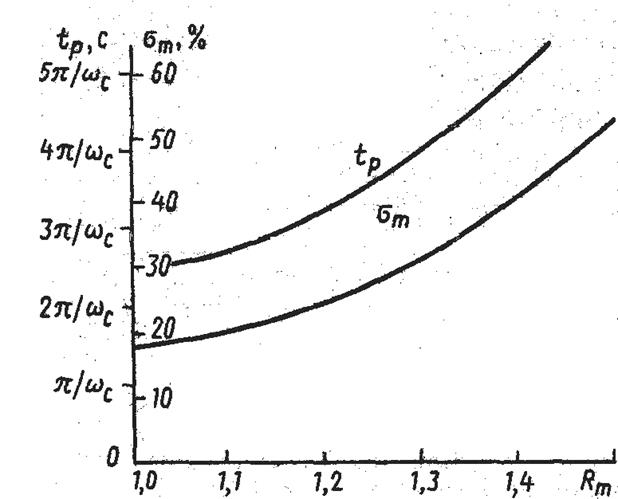
Рисунок 7 – Монограмма Солодовникова
По монограмме Солодовникова определяется время регулирования
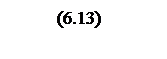
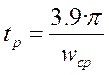 ,
,
где tp – время регулирования, с;
wcp – частота среза системы, с-1.
По выражению (6.13) определим частоту среза системы
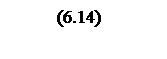
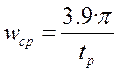 ,
,
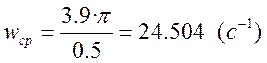 .
.
Переходя к псевдочастоте
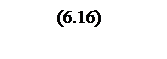
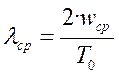 ,
,
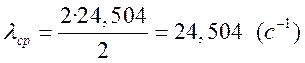 .
.
Определяется параметр
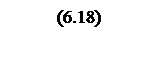
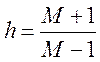 ,
,
где M=1,3 показатель колебательности системы.
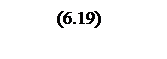
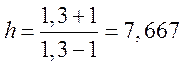 .
.
Определяются частоты сопряжения
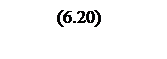
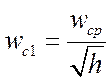 ,
,
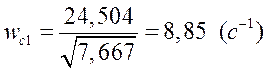 ,
,
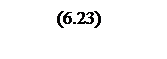
![]() ,
,
![]() .
.
При переходе к псевдочастоте
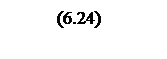
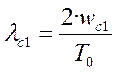 ,
,
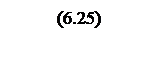
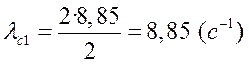 ,
,
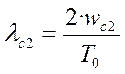 ,
,
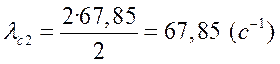 .
.
Желаемая ЛАЧХ системы совместно с исходной ЛАЧХ изображена на рисунке 8.
По виду построенной ЖЛАЧХ определяется передаточная функция желаемой разомкнутой системы
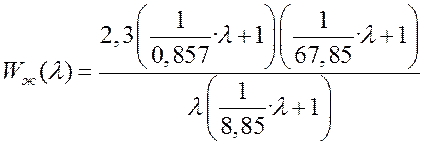 .
.
Действительные и мнимые части которой
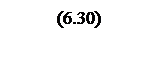
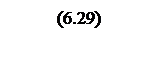
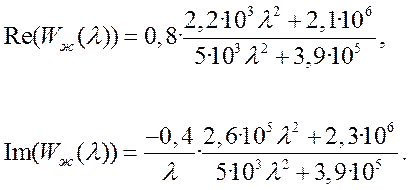
АЧХ желаемой системы
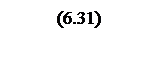
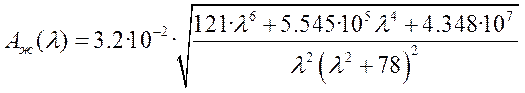 .
.
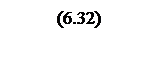 ЖЛАЧХ системы
ЖЛАЧХ системы
![]() ,
,
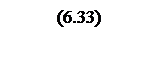
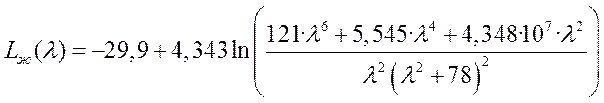 .
.
ЖЛФЧХ системы
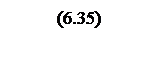
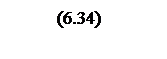
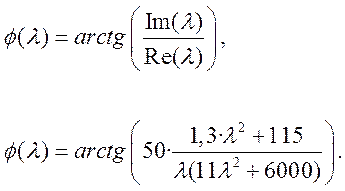
ЖЛФЧХ системы изображена на рисунке 8.
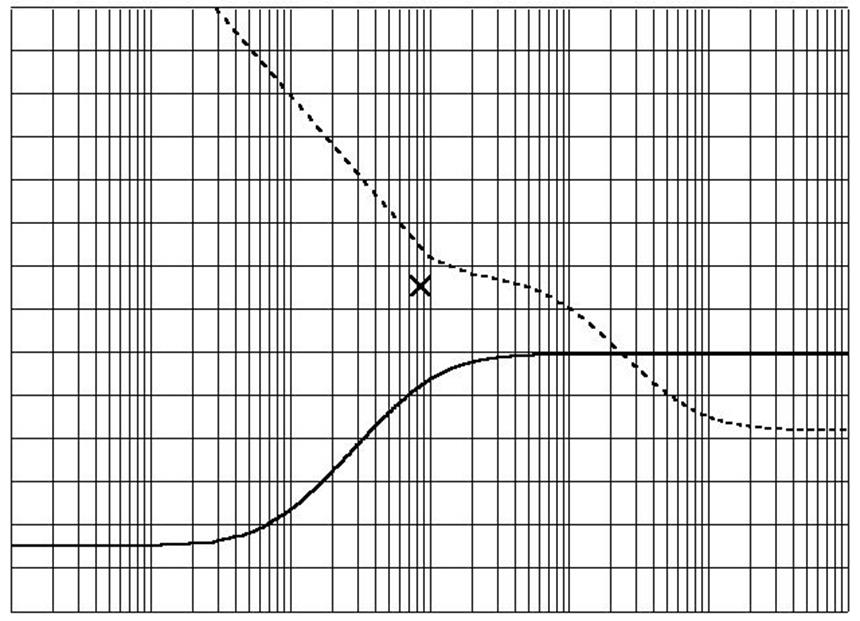

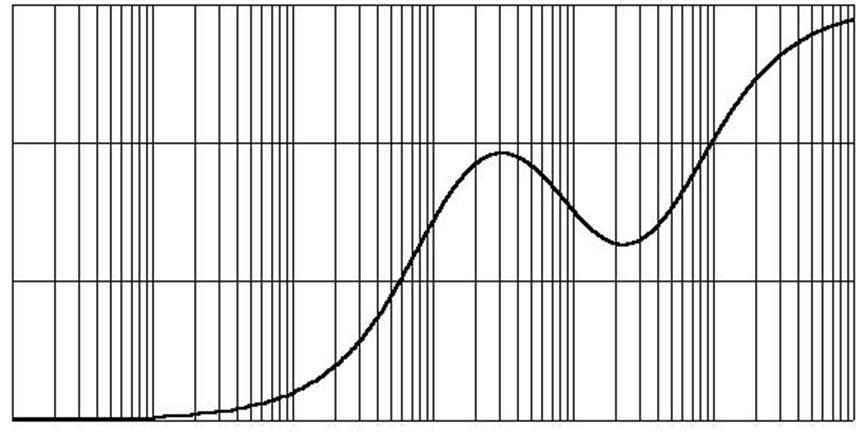
Рисунок 8 – ЖЛАЧХ и ЖЛФЧХ системы
По ЛАЧХ и ЛФЧХ видно, что запас устойчивости по амплитуде равен бесконечности и фазе ψ=1800-520=1280.
ЛАЧХ последовательного корректирующего устройства (КУ) вычисляется
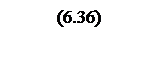
![]() .
.
Вид ЛАЧХ КУ представлен на рисунке 9.
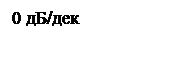
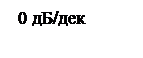
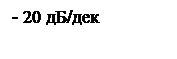
![]()
![]()
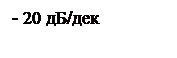
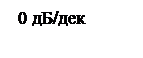

![]()

![]()
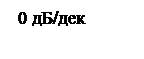
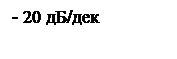
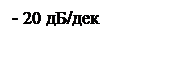
![]()


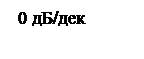
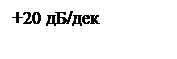
![]()
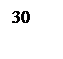
![]()
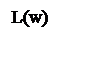
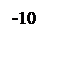
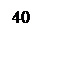
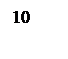
![]()
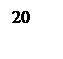
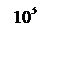
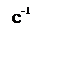
![]()
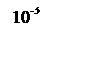
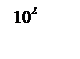
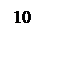
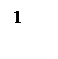
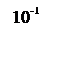
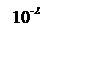 Рисунок 9 - ЛАЧХ
последовательного КУ
Рисунок 9 - ЛАЧХ
последовательного КУ
Передаточная функция желаемой системы с обратной единичной отрицательной связью
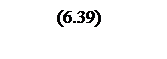
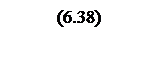
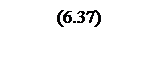
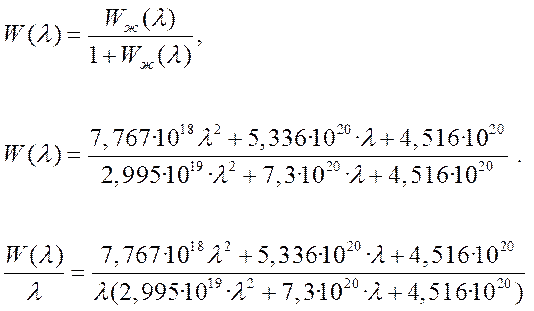
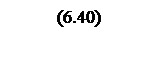 Разложим выражение (6.39)
на правильные дроби
Разложим выражение (6.39)
на правильные дроби
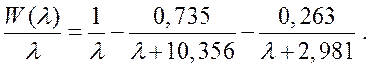
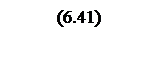 Для получения
переходной функции выполняется обратное преобразование Лапласа от выражения (6.40),
по табличным формулам [7]
Для получения
переходной функции выполняется обратное преобразование Лапласа от выражения (6.40),
по табличным формулам [7]
![]()
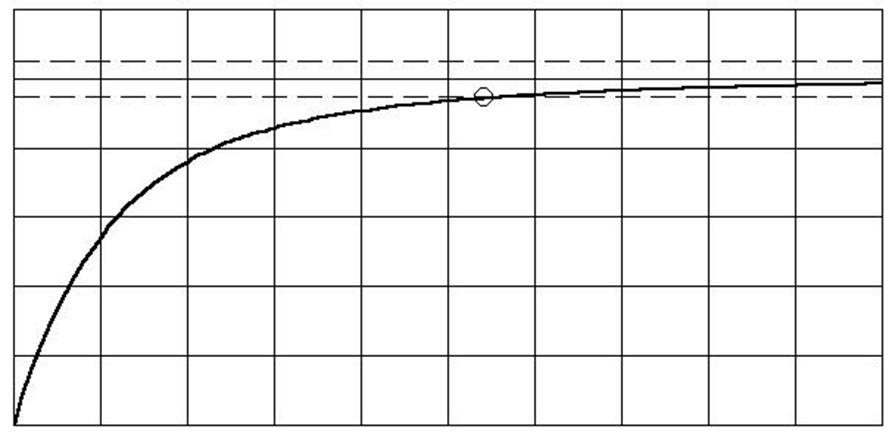
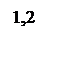 Переходный процесс желаемой замкнутой системы изображён на рисунке 10.
Переходный процесс желаемой замкнутой системы изображён на рисунке 10.

![]()
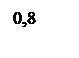
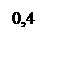
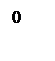
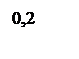
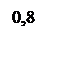
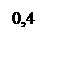
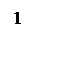
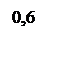
 |
Рисунок 10 – Переходный процесс желаемой системы
По переходному процессу видно что время перерегулирования составляет 0,54 с, что соответствует ТЗ. Однако перерегулирование в 25 процентов не добились.
7 Расчёт корректирующего устройства. Использование дискретного корректирующего устройства
По ЛАЧХ КУ (рисунок 9) строится передаточная функция последовательного непрерывного корректирующего устройства
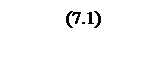
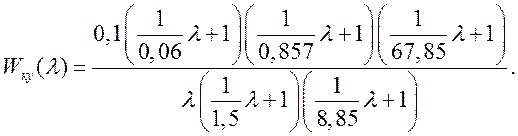
Проектируемая ЛСАУ является электрической поэтому реализацию КУ целесообразно выполнять на электрических элементах в виде пассивных четырёхполюсников. Для проектирования КУ по выражению (7.1), необходимы два вида пассивных четырёхполюсника. Принципиальная схема интегрирующего представлены на рисунке 11.
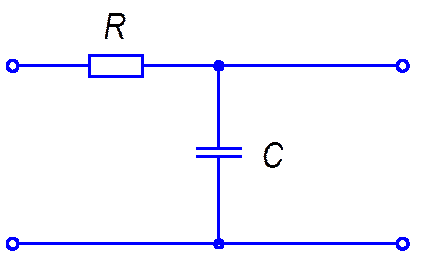
Рисунок 11– Схема электрическая принципиальная интегрирующего звена КУ
Передаточная функция интегрирующего звена
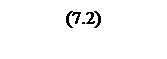
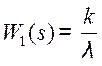 .
.
ЛАЧХ интегрирующего звена представляет собой прямую с наклоном -20 дБ/дек.
Следующее электрическая схема представляет собой четырёхполюсник вид которого на рисунке 12.
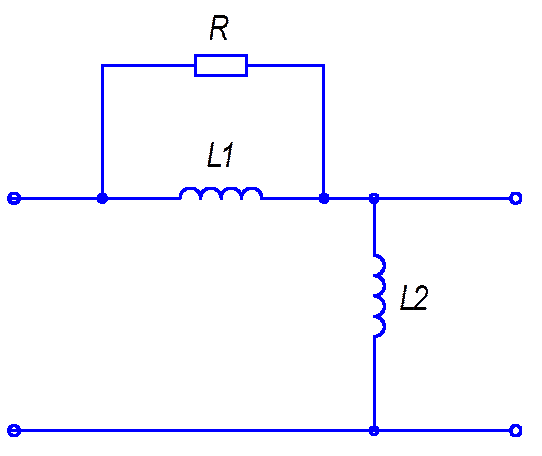
Рисунок 12 – Схема электрическая принципиальная части КУ
Передаточная функция КУ с принципиальной схемой по виду рисунка 12.
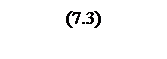
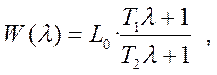
где
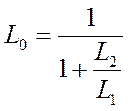 - коэффициент передачи;
- коэффициент передачи;
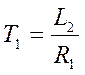 - постоянная времени форсирующего звена;
- постоянная времени форсирующего звена;
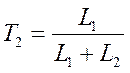 - постоянная времени апериодического
звена.
- постоянная времени апериодического
звена.
ЛАЧХ КУ по принципиальной схеме рисунка 12 представляет собой ломанную прямую с последовательными наклонами 0,+20, 0 дБ/дек.
Составляется передаточная функция КУ.
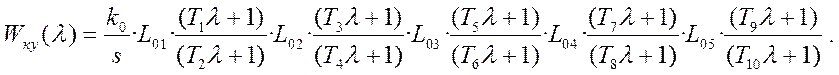
Оценим коэффициенты и постоянные времени
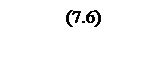
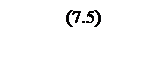
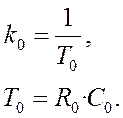
Интегрирование осуществляется при достаточно большой постоянной времени интегрирования, поэтому выберем значения параметров следующими
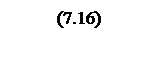
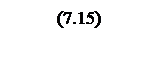
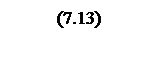
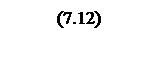
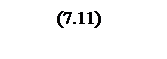
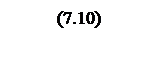
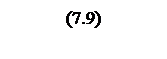
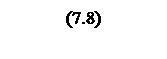
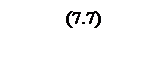
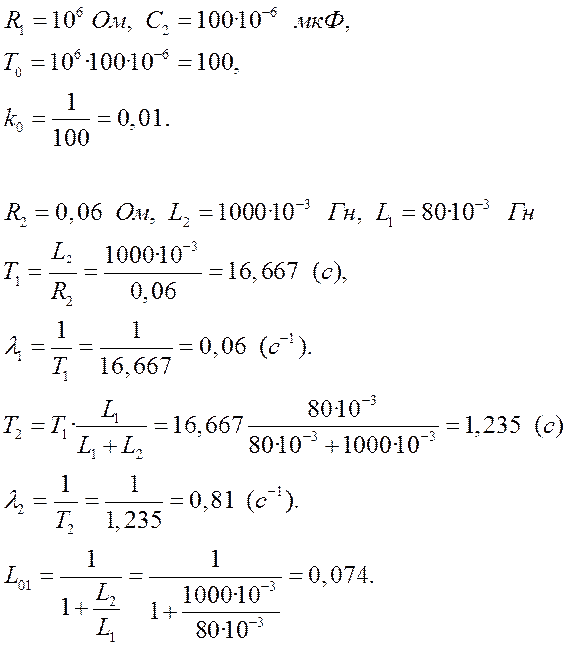
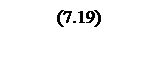
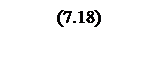
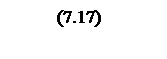
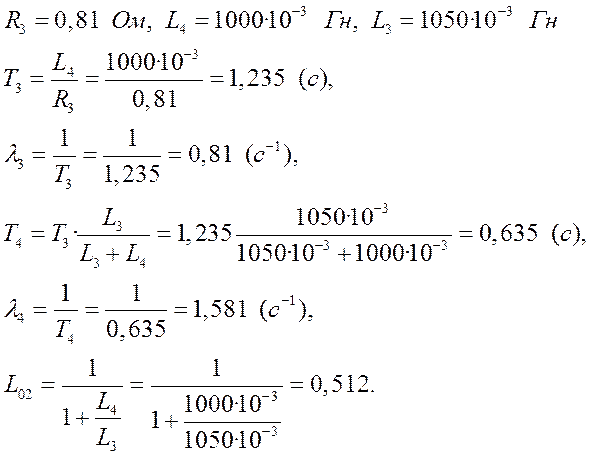
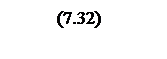
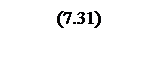
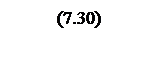
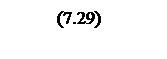
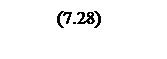
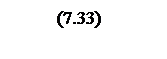
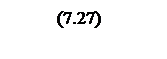
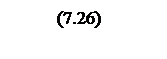
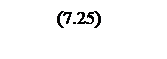
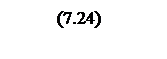
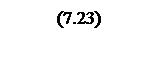
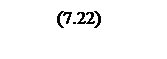
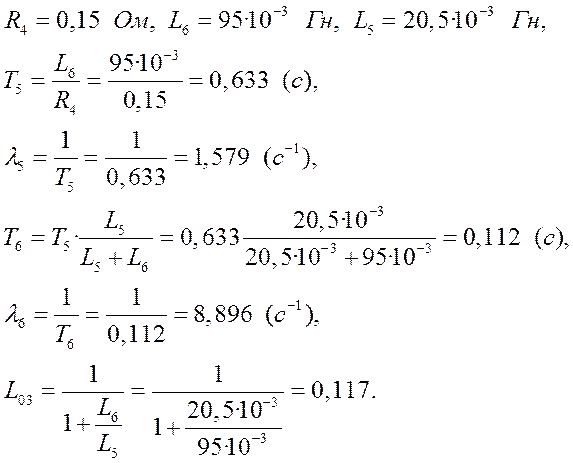
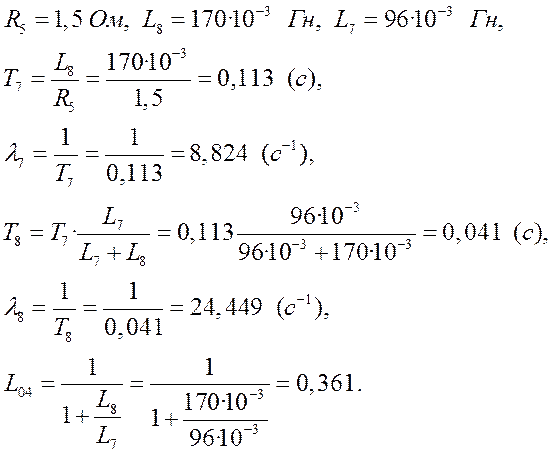
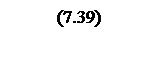
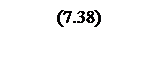
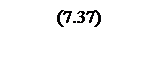
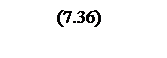
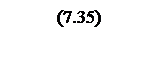
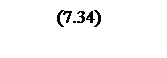
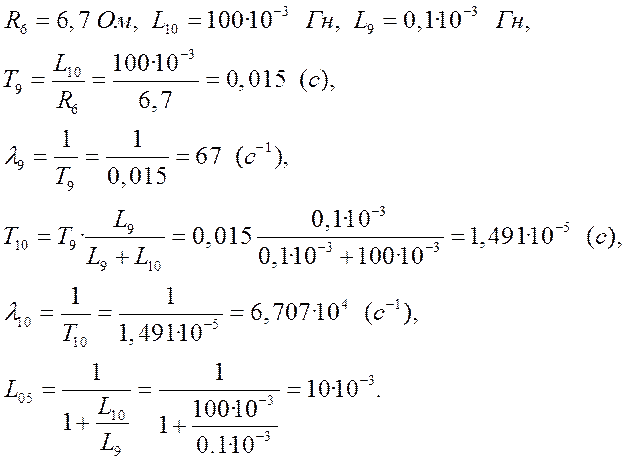
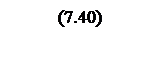 Тогда общий
коэффициент передачи КУ
Тогда общий
коэффициент передачи КУ
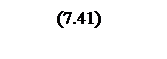
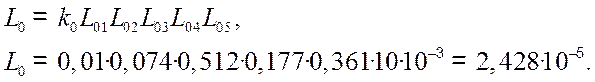
 Необходимо
компенсировать влияния коэффициента ослабления, поэтому коэффициент усиления
усилителя
Необходимо
компенсировать влияния коэффициента ослабления, поэтому коэффициент усиления
усилителя
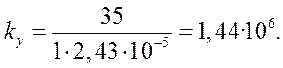
Реализуется такой коэффициент усиления при
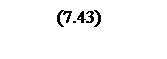
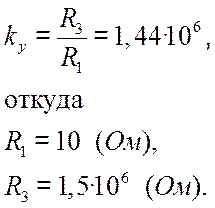
Дискретное корректирующее устройство реализуется в виде программа для МПС. Для получения программы необходимо конечноразностное уравнение.
Передаточная функция корректирующего устройства
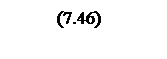
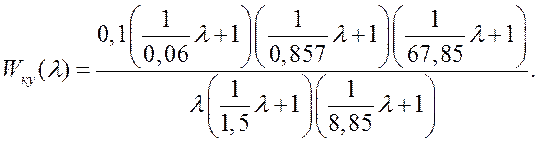
Проводится обратное билинейное преобразование
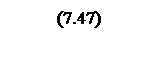
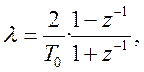
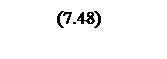
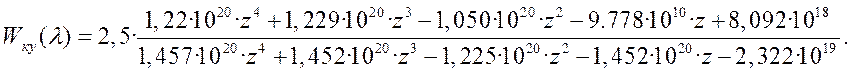
Или
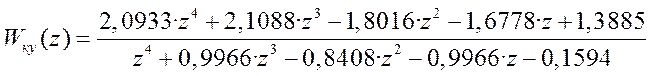 .
.
 Разделим числитель и
знаменатель на z-4
Разделим числитель и
знаменатель на z-4
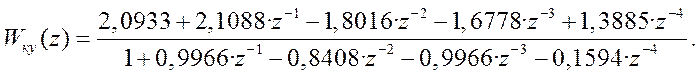
По полученному выражению записывается разностное уравнение в реальном масштабе времени, введя в числитель дополнительный сдвиг на z-1
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.