Проектирование локальной системы глубоководного манипулятора бурения донной поверхности для взятия проб грунта, страница 7

По выражению (4.14) видно что корни характеристического уравнения находятся внутри единичной окружности, что свидетельствует о устойчивости дискретной системы.

5 Построение ЛАЧХ системы и её анализ

Для построения функции слежения за частотой выходного вала в проектируемой ЛСАУ в цепь обратной отрицательной связи включён преобразователь, который преобразует текущую частоту на выходном валу в напряжение. Тахогенератор выполняет преобразование величин по закону

,

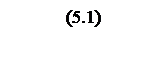
где    k_тг=0,22 B/c – крутизна характеристики тахогенератора;

Ω – текущая частота вращения выходного вала.

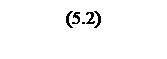Сигнал с тахогенератора сравнивается с сигналом задатчика частоты вращения реализованным программно в МПС. Задатчик преобразует числовой код частоты вращения заданный программно  в числовой код напряжения

,

где     k_з – коэффициент преобразования задатчика;

ω – заданная частота вращения выходного вала.

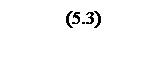Измеритель рассогласования (ИР), выполненный  также программно, вычисляет отклонение сигнала от  заданного. На выходе ИР имеется сигнал

.

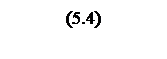Для построения ЛАЧХ разомкнутой  и анализа системы необходимо наличие обратной единичной отрицательной связи, для этого, учтя рассуждения выше, реализуем программно выполнение условия

.

Тогда

.

где    δ – отклонение текущей частоты от заданной.

В результате структурная схемы проектируемой ЛСАУ примет вид  рисунка 5.

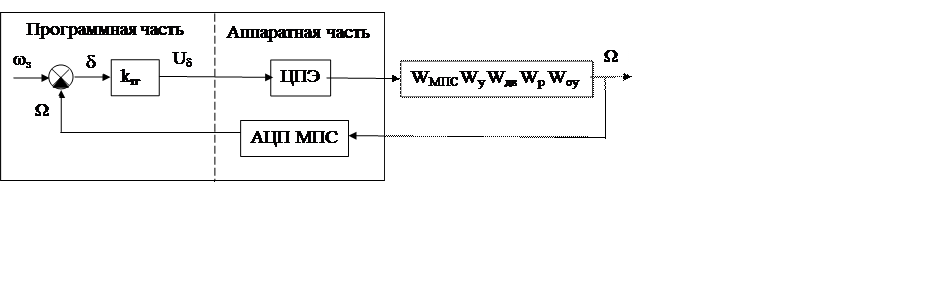
Рисунок 5 – Структурная схема ЛСАУ

Тогда передаточная функция разомкнутой системы

.

Или при подстановке выражений для передаточной функции

,

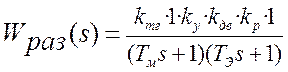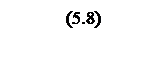Окончательно передаточная функция разомкнутой системы

.

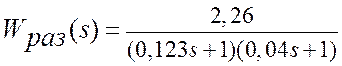Для получения Z формы передаточной функции выполняется следующее

.

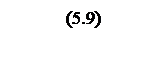
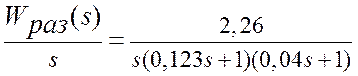Табличная формула перехода к Z форме по полученному выражению (5.9) в форме изображения по Лапласу

.

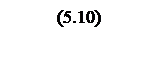
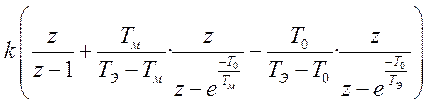Тогда передаточная функция разомкнутой системы в Z форме

.

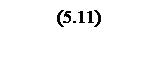
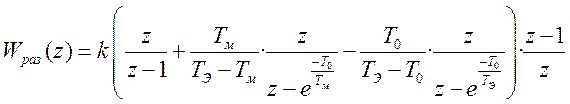После подстановки коэффициентов и упрощения передаточная функция примет вид

.

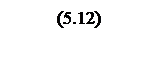
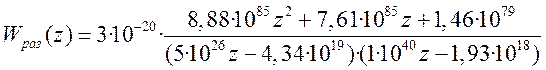Для построения ЛАЧХ делается билинейное преобразование, для этого осуществляется подстановка

.

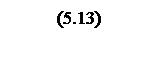
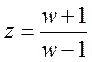После подстановки и упрощения передаточная функция

.

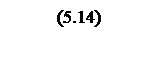
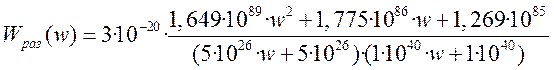Переходя к псевдочастоте передаточная функция

.

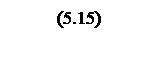
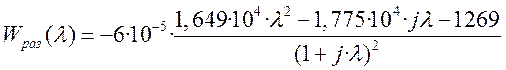Действительная часть передаточной функции

.

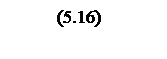
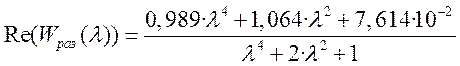Мнимая часть передаточной функции

.

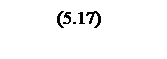
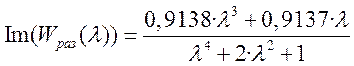Амплитудночастотная характеристика системы

.

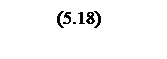
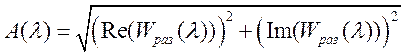При подстановке в (5.18) выражений мнимой и действительной частей

.

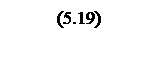
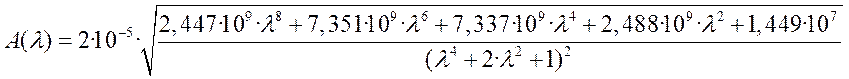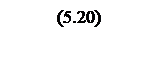ЛАЧХ разомкнутой системы вычисляется

.

При вычислении и упрощении выражение (5.20) примет вид

.

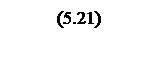
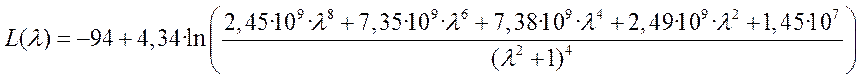ЛФЧХ системы определяется

.

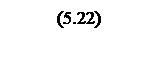
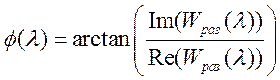При вычислении и упрощении выражение (5.22) примет вид

.

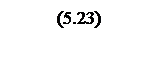
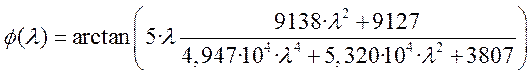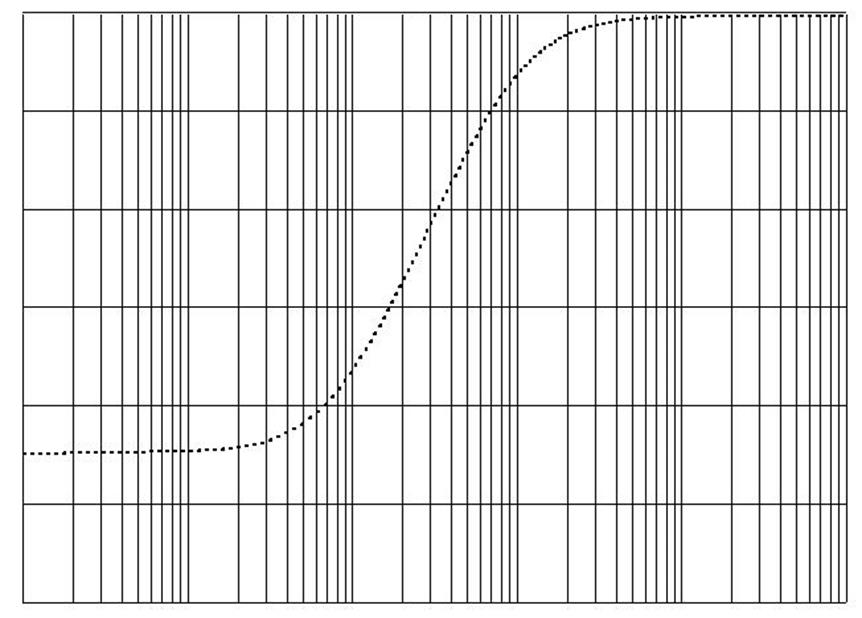
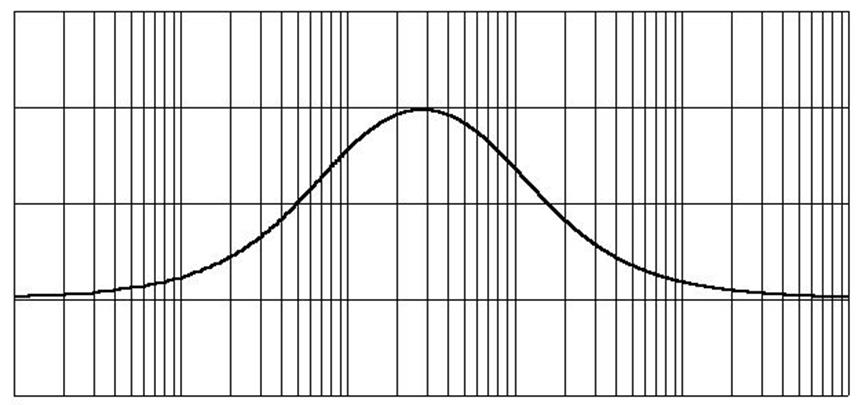
ЛАЧХ  и ЛФЧХ разомкнутой системы изображены на рисунке 6.

 

 

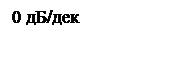
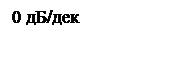
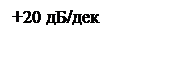
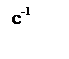
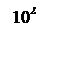
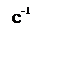
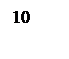
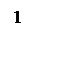
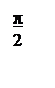
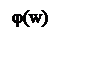
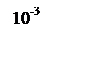
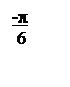
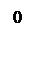
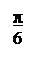
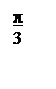
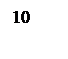
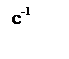
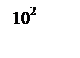
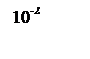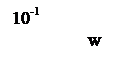Рисунок 6 – ЛАЧХ и ЛФЧХ системы.

По ЛАЧХ и ЛФЧХ видно что запас устойчивости по амплитуде и фазе равны бесконечности.

6 Построение ЖЛАЧХ системы, ЛАЧХ корректирующего устройства

Для построения ЖЛАЧХ определяется  рабочая точка (РБ) системы.

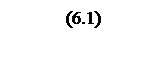Пусть на входе системы (задатчик) действует частота изменяющаяся по закону

,

где    w₀ – амплитудное  частоты на входе системы, 1/с;

w₁ – частота изменения сигнала на входе, 1/с;

Скорость изменения частоты вращения вала

.

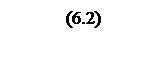
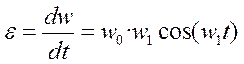Ускорение частоты  вращения вала

.

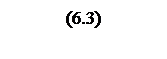
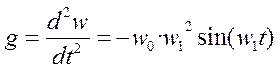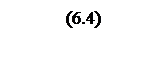Введём обозначение

,

,

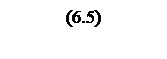
где    ε₀ – амплитуда скорости изменения частоты вращения вала, 1/с²;

ε_Н – ускорение в нагрузке, 1/с²;

g₀ – амплитуда ускорения изменения частоты вращения вала, 1/с³;

g_H – скорость изменения ускорения в нагрузке, 1/с³.

Тогда рабочая частота системы

,

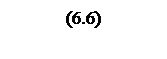
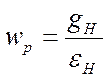где     g_H=1,8 с^-3 – скорость ускорения в нагрузке;

ε_Н=2,1с^-2 – ускорение в нагрузке, 1/с².

.

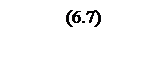
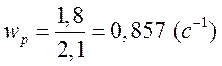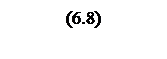При переходе к псевдочастоте

.

 

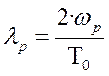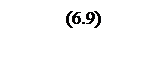
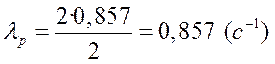
Частота качания на входе системы

.

.

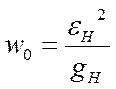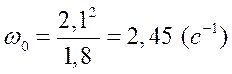В логарифмическом масштабе

,

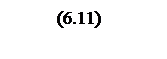
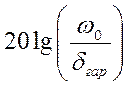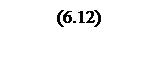где    δ_гар – заданная в ТЗ точность управления, с^-1.

.

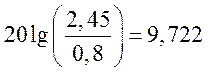Окончательно РБ имеет координаты (0,857;9,722).

По ТЗ система в динамическом  режиме должна удовлетворять следующим условиям: