ФАКУЛЬТЕТ ИНЖЕНЕРНО-СТРОИТЕЛЬНЫЙ
КАФЕДРА УПРАВЛЕНИЕ И ИНФОРМАТИКА В ТЕХНИЧЕСКИХ СИСТЕМАХ
по дисциплине
Локальные системы управления
Выполнил ст. гр. УИТ-51
Колесникова Е.В.
Принял
Ефремова Т.А.__________
«____» _____________2004г.
2004
Вариант 10.
Найти передаточную функцию СУ. Построить переходный процесс системы. Исследовать устойчивость СУ по одному из критериев. По переходному процессу провести анализ качества управления и определить все его показатели. Оценить систему на устойчивость любым из критериев. Построить ЛАЧХ системы:
а) Построить желаемую ЛАЧХ системы методом Солодовникова
б) методом запретной зоны
в) графическим методом
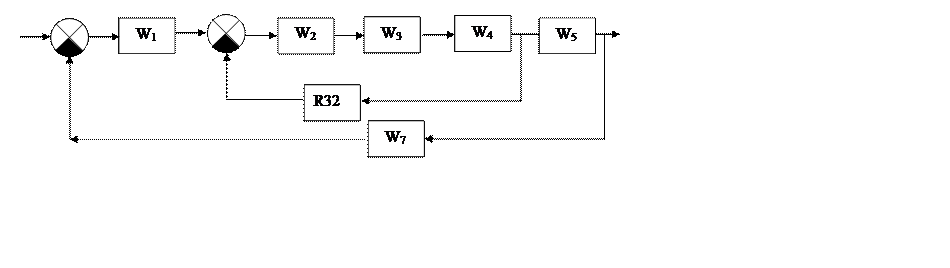
Рисунок 1
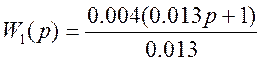
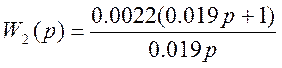
![]()
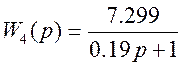
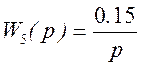
![]()
![]()
Изобразим логарифмическую амплитудно-частотную характеристику для разомкнутой системы:
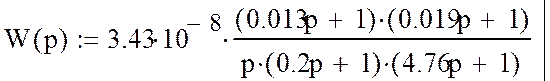
Построим желаемую ЛАЧХ методом Солодовникова
По номограмме Солодовникова (Рисунок 4) и желаемому перерегулированию ![]() , колебательности (М=1.3) и времени
регулирования (tр=0.9 c) определяем частоту
среза:
, колебательности (М=1.3) и времени
регулирования (tр=0.9 c) определяем частоту
среза:
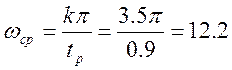 (рад). lg(
(рад). lg(![]() )=1.1
)=1.1
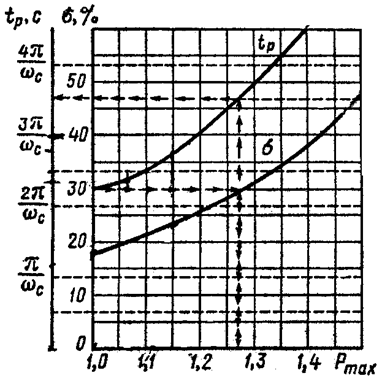 Рисунок 4 - Номограмма
Солодовникова
Рисунок 4 - Номограмма
Солодовникова
Для того чтобы система была устойчива и отвечала заданным критериям
качества необходимо, чтобы через точку на оси абсцисс с координатой wср она проходила с наклоном минус
20 дБ/дек до пересечения с асимптотами 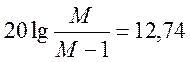 дБ и
дБ и 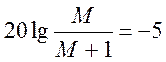 дБ, а за пределами асимптот наклон будет составлять
минус 40 дБ/дек и минус 20 дБ/дек.
дБ, а за пределами асимптот наклон будет составлять
минус 40 дБ/дек и минус 20 дБ/дек.
1) ЛАЧХ последовательного корректирующего звена определяется путем вычитания из ЖЛАЧХ ЛАЧХ неизменяемой части:
![]() .
.
Желаемая передаточная функция:
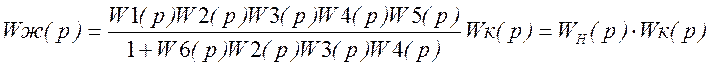
По построенной ![]() найдём частоты сопряжения и
соответствующие им постоянные времени:
найдём частоты сопряжения и
соответствующие им постоянные времени:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
По виду полученной логарифмической амплитудно-частотной характеристики корректирующего устройства находим его передаточную функцию:
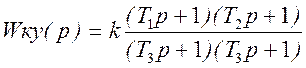 ,
,
где 20lgk=180 дБ, т.е. k=109.
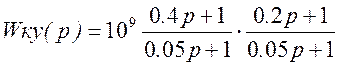
Полученной передаточной функции КУ можно поставить в соответствие усилитель с Ку=109 и 2 последовательно соединённых КУ:
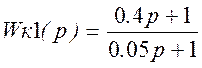 ,
,
где![]() ,
, ![]()
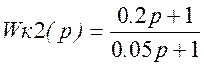 ,
,
где![]() ,
, ![]()
По справочнику находим вид КУ:
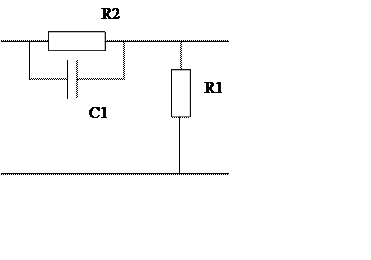 |
Рассчитаем параметры корректирующего устройства.
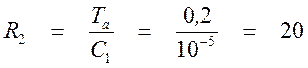
Задаемся значением С1=10 мкФ. Тогда для ![]() :
:
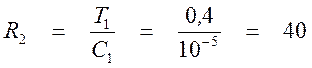 (кОм),
(кОм),
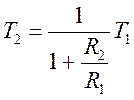 , откуда
, откуда 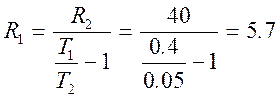 (кОм)
(кОм)
При С1=10 мкФ для ![]() :
:
 (кОм),
(кОм),
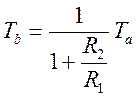 , откуда
, откуда 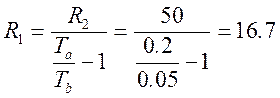 (кОм).
(кОм).
По передаточной функции исходной системы построим график переходного процесса h(t) (рисунок 1).
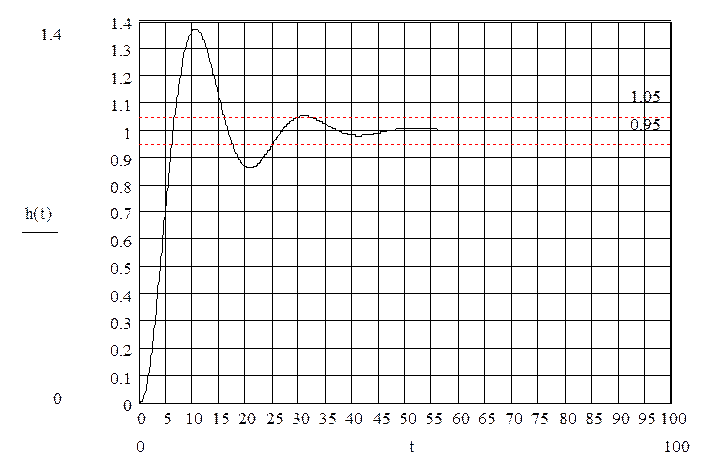
Рисунок 1
По полученному переходному процессу определяем прямые показатели качества управления СУ.
1 Установившееся значение. По графику hуст=1.
Вокруг hуст выделим область с допуском D=5% от hуст: D=0.05 hуст=0.05
Тогда 5% интервал отклонения от установившегося значения будет соответствовать следующим величинам.
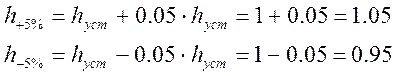
2 Время регулирования (время переходного процесса) – время, в течение которого переходная функция достигает установившегося значения с допуском 5%. tp=25 с.
3
Перерегулирование 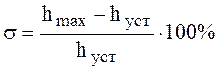
По графику ![]() , тогда:
, тогда: 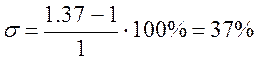
4 Колебательность - число колебаний за время регулирования. n=1.
5 Время нарастания регулируемой величины - время достижения максимума. tн=11c.
6 Время первого согласования – время, когда регулируемая величина в первый раз достигает своего установившегося значения. t1=27 c.
По желаемой передаточной функции построим график переходного процесса h(t) (рисунок 2).
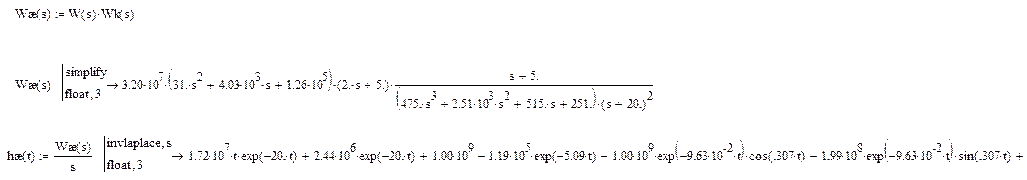
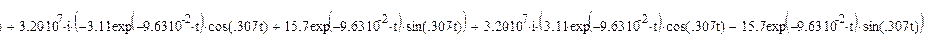
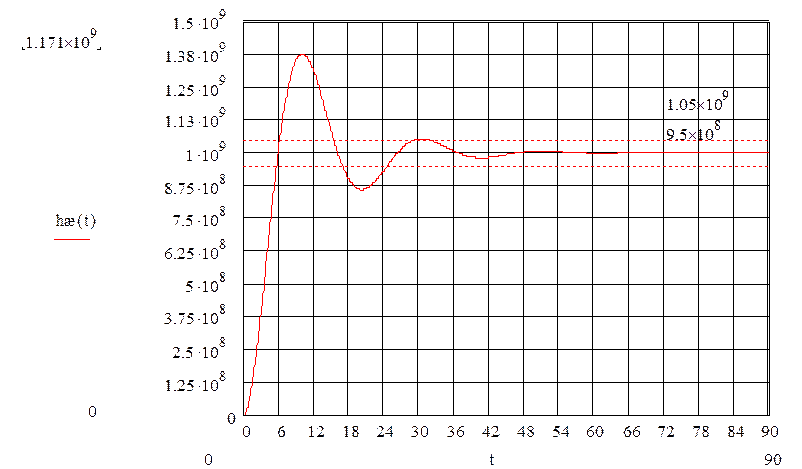
Рисунок 2
По полученному переходному процессу определяем прямые показатели качества управления СУ.
1 Установившееся значение. По графику hуст=109. (Вокруг hуст выделим область с допуском D=5% от hуст)
2 Время регулирования (время переходного процесса) – время, в течение которого переходная функция достигает установившегося значения с допуском 5%. tp=24 с.
3
Перерегулирование 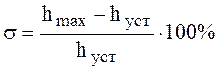 .
. 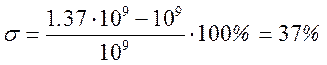
4 Колебательность - число колебаний за время регулирования. n=1.
5 Время нарастания регулируемой величины - время достижения максимума. tн=11c.
6 Время первого согласования – время, когда регулируемая величина в первый раз достигает своего установившегося значения. t1=10 c.
2) Построение логарифмической амплитудно-частотной характеристики встречно-параллельного корректирующего устройства
Для замкнутого контура передаточная функция запишется как:
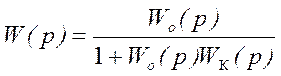
Так как W0WK>>1, то пренебрегая 1-цей с некоторой малой погрешностью можно записать, что Wk=1/Wж. Это значит, что ЛАЧХ параллельного корректирующего звена может быть получена из ЖЛАЧХ домножением ее на минус 1:
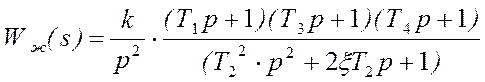
20lg(k)=30, отсюда к=31.6
![]()
По построенной ![]() найдём частоты сопряжения и
соответствующие им постоянные времени:
найдём частоты сопряжения и
соответствующие им постоянные времени:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
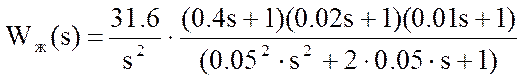
Следовательно, получаем передаточную функцию встречно-параллельного корректирующего звена в виде:
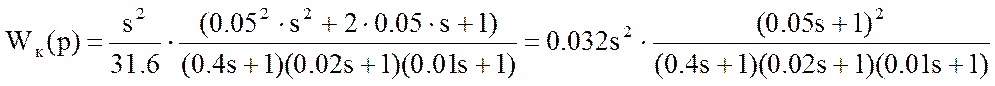
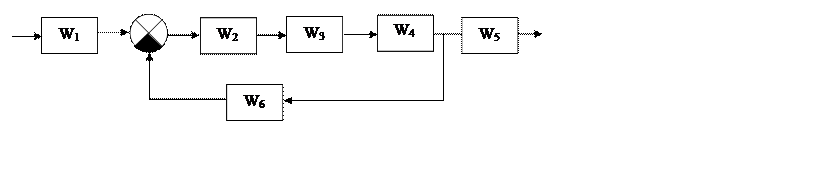
Изобразим схему последовательного соединения:
- форсирующего ![]() (1,2,6)
(1,2,6)
- форсирующего и
инерционного звеньев 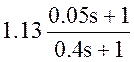 (1,2,11)
(1,2,11)
- двух
дифференцирующих и двух инерционных звеньев 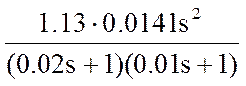 (1,2,28)
(1,2,28)
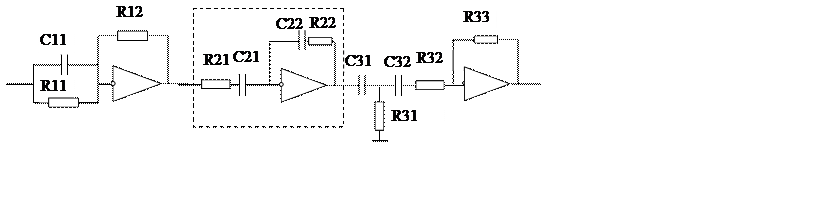
Зададим R11=10кОм
R12/ R11=1, откуда R12=10кОм
0.05= R11* C11, откуда C11=5мкФ
Зададим C21=6мкФ
0.4=C21/C22, откуда C22=15мкФ
0.05= R22*C22, откуда R22=3.333кОм
0.4=R21*С21, откуда R21=67кОм.
Зададим C32=2мкФ, R31=6кОм
R33/C32=1.13, откуда R33=2,26МОм
0.0002=R31*R32*C31*C32, откуда C22=15мкФ
0.03=R31*C31+R32*C32-R31*C32
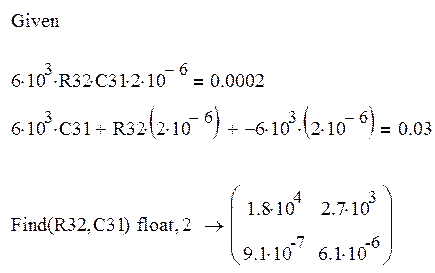
3) Построение логарифмической амплитудно-частотной характеристики параллельного корректирующего устройства
Используем формулу перехода от последовательного КУ к параллельному. Передаточная функция параллельного КУ через передаточную функцию последовательного КУ W(s):
![]()
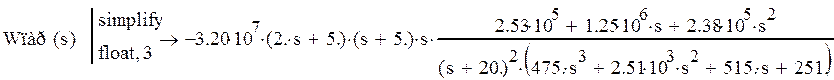
или после тождественных преобразований
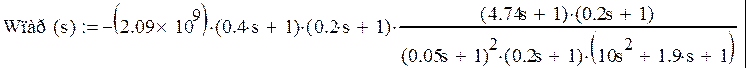
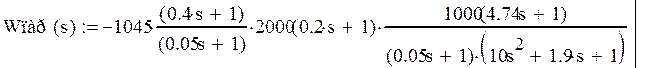
Изобразим схему последовательного соединения:
- форсирующего ![]() (1,2,6)
(1,2,6)
- форсирующего и
инерционного звеньев 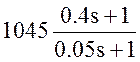 (1,2,11)
(1,2,11)
- последовательного
соединения форсирующего, инерционного и колебательного звеньев 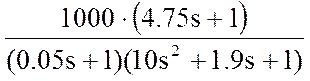 (1,2,27)
(1,2,27)
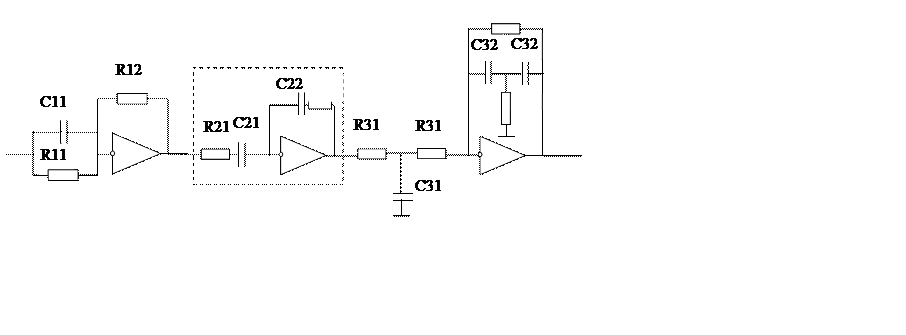
Зададим R11=200 Ом
R12/ R11=2000, откуда R12=4МОм
0.2= R11* C11, откуда C11=1мФ
Зададим C21=6мкФ
1045=C21/C22, откуда C22=6,27мФ
0.4= R22*C22, откуда R22=67кОм
0.05=R21*С21, откуда R21=8.3кОм.
Зададим C31=10мкФ, R31=6кОм
0.05=R31*C31, откуда R31=5кОм
1000=2*R32/R31, откуда R32=2.5МОм
1.9=R32*C32, откуда C32=0.76мкФ.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.