Построение желаемой ЛАЧХ методом запретной зоны

ПОСТРОЕНИЕ ЖЛАЧХ МЕТОДОМ ЗАПРЕТНОЙ ЗОНЫ

Цель работы: Ознакомление с методикой построения желаемой ЛАЧХ методом запретной зоны  для синтеза линейных систем автоматического управления с заданными показателями качества. (скорость и ускорение изменения сигнала, а также колебательность)

ОСНОВНЫЕ ПОНЯТИЯ

Оценка качества по показателю коле­бательности.

Показатель колебательности M определятся из АЧХ замкнутой системы как

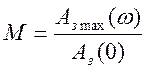, и характеризует склонность системы к колебаниям. Чем выше М, тем менее качественна система при прочих равных условиях. Считается допустимым, если 1.1 ≤ M ≤ 1.5.

Если АЧХ системы при нулевой частоте равна 1, то показатель колебательности

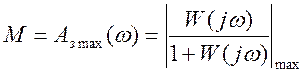
где W(jω) – передаточная функция разомкнутой системы.

          Чтобы определить   показатель      колебательности     системы,

можно воспользоваться амплитудно-фазовой частотной харак­теристикой разомкнутой системы W(jω)=u(ω)+jv(ω), где u(ω)=ReW(jω), v=ImW(jω).

   Показатель колебательности можно вычислить так:

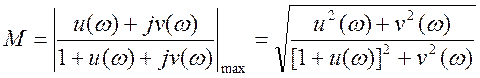
Возведя в квадрат обе части равенства, получим

После алгебраических преобразований можно записать

Полученное выражение является центром окружности с радиусом R=M/(M²-1) и центром, смещенном от начала координат влево на величину С=M²/(M²-1). Задаваясь различными значениями М от 0 до ∞, можно построить се­мейство таких окружностей. При М=1 окружность вырождается в прямую (R à ∞, C à ∞ ), параллельную мни­мой оси и проходящую через точку (-0,5, j0).

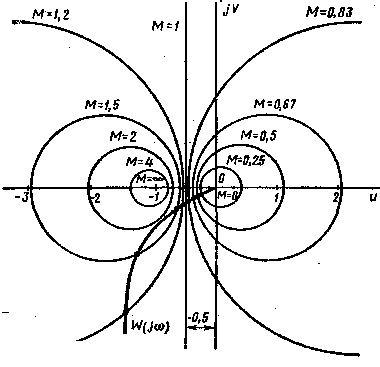
При 0<M<l окруж­ности располагаются справа от линии, соответствующей М = 1, а при М > 1 - сле­ва от нее. Если M à ∞, то окружность вырождается в точку с координатами [—1, j0]. Номограммы можно ис­пользовать для построения амплитудно-частотной харак­теристики замкнутой системы A_з(ω). Для этого на номограм­му наносят амплитудно-фазо­вую характеристику ра­зомкнутой системы W(jω), далее по точкам пересечения последней с окружностями определяют значения A_з(ω). Ког­да нужно оценить значение показателя колебательности M, то строить амплитудно-фазовую характеристику не нужно, а не­обходимо только оценить, какой наименьшей окружности она коснется; значение М = const, соответствующее этой окружности, и будет показателем колебательности.

При проектировании системы может быть поставлено усло­вие, чтобы показатель колебательности М не превышал за­данного значения. Это значение определяет ту запретную об­ласть, куда не должна заходить амплитудно-фазовая характе­ристика разомкнутой системы W(jω).

 

 

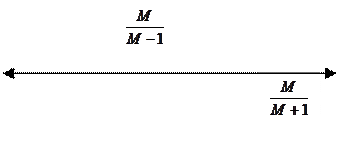
Таким образом, для обеспечения заданной колебательности М среднечастотная асимптота разомкнутой системы должна иметь наклон -20 дБ/дек, при изменении u(ω) от M/(M-1) до M/(M+1).

Понятие рабочей точки.

Если на вход системы подается гармонический сигнал β= β₀sin(ωt), cкорость изменения сигнала составит g’= dβ/dt= β₀ω∙cos(ωt), откуда β₀ω – амплитуда угловой скорости.

Ускорение изменения сигнала g’’= d²β/dt²= β₀ω² ∙(-sin(ωt)), откуда β₀ω² – амплитуда углового ускорения.

В режиме поддержания заданной скорости изменения сигнала g’ и ускорения g’’, можно записать g’’= β₀ω²; g’= β₀ω, тогда

ω_р= g’’/ g’ – рабочая частота

β₀= g’²/ g’’ – рабочая амплитуда

            Величины ω_р и β₀ вычислены через заданные скорость и ускорения сигнала, ограничения на которые могут накладывать характеристики звеньев системы или заданный закон регулирования.

            Если ЛАЧХ разомкнутой системы проходит выше рабочей точки, то система обеспечивает все заданные для нее параметры, если рабочая точка оказывается выше ЛАЧХ то требования не выполняются и система требует коррекции.

Построение желаемой ЛАЧХ.

Желаемой называют асим­птотическую ЛАЧХ разомкнутой системы, имеющей  желаемые (требуемые) статические и динамические свойства. Желаемая ЛАЧХ состоит из трех основных асимп­тот: низкочастотной, среднечастотной и высокочастотной. Кроме того, могут быть сопрягающие асимптоты, которые со­единяют основные.

Строится желаемая ЛАЧХ на основании требований к си­стеме.

Низкочастотная асимптота ЛАЧХ разомкнутой системы определяет статические свойст­ва.

Среднечастотная асимптота ЛАЧХ разомкнутой системы и ее сопряжение с низкочастотной определяют динамические свойства системы — устойчивость и показатели качества пе­реходной характеристики.

       Высокочастотная асимптота желаемой ЛАЧХ мало влияет на свойства системы, поэтому со следует выбирать так, чтобы корректирующее устройство было возможно более простым. Это достигается при совмещении высокочастотных асимптот характеристик исходной и желаемой ЛАЧХ. Если совмещение не удается, то высокочастотная асимптота ЖЛАЧХ должна иметь тот же на­клон, что и высокочастотная асимптота ЛАЧХ.

Построение желаемой ЛАЧХ методом запретной зоны начинается с нахождения рабочей точки системы, затем через нее проводится сопрягающая асимптота с наклоном -40 дБ/дек, до пересечения с верхним уровнем 20lg[M/(M-1)].

 Для обеспечения заданной колебательности М строится среднечастотная асимптота, которая имеет наклон -20 дБ/дек, и продолжается  до пересечения с нижним уровнем 20lg[M/(M+1)]. При пересечении асимптоты с нулевым уровнем определяется требуемая частота среза ω_ср скорректированной системы.

Низкочастотная асимптота ЖЛАЧХ продолжается до рабочей точки и должна иметь тот же на­клон, что и низкочастотная асимптота ЛАЧХ.

Высокочастотная асимптота ЖЛАЧХ начинается на уровне 20lg[M/(M+1)] и должна иметь тот же на­клон, что и высокочастотная асимптота ЛАЧХ.

 Построение желаемой ЛАЧХ основано на опреде­ленных допущениях. Кроме того, могла иметь место прибли­женная реализация требуемой ЛАЧХ корректирующего уст­ройства. Поэтому совершенно необходима проверка качест­ва синтезированной системы. С этой целью строится переход­ная характеристика замкнутой системы и определяются пока­затели ее качества.