Применение пакета Сontrol System Toolbox, входящего в программу MATLAB

При проектировании систем автоматического управления и регулирования, как непрерывных, так и дискретных, требуется провести исследование динамических свойств системы, основанное на использовании передаточных функций. Для этого  служат графики, отражающие частотные и временные характеристики, а также положение нулей и полюсов системы.

В состав программы MATLAB входит пакет Сontrol System Toolbox, предназначенный для моделирования, анализа и проектирования САР и САУ.
                              В пакете реализованы:

- обширный набор средств для анализа одномерных и многомерных динамических систем (объектов);

- построение основных характеристик систем: импульсной, передаточной и переходной, реакция на произвольное воздействие;

- построение частотных характеристик: ЛАЧХ и ЛФЧХ, диаграмм Найквиста, Николса;

- разработка замкнутых систем регулирования;

- проектирование регуляторов.

Интерактивная среда для отображения временного и частотного отклика предоставляют пользователю графические управляющие элементы для одновременного отображения данных откликов и переключение между ними. Можно вычислять различные характеристики откликов, такие, например как время регулирования.

Рассмотрим пример проектирования системы автоматического управления, неизменяемая часть которой представлена на рисунке:

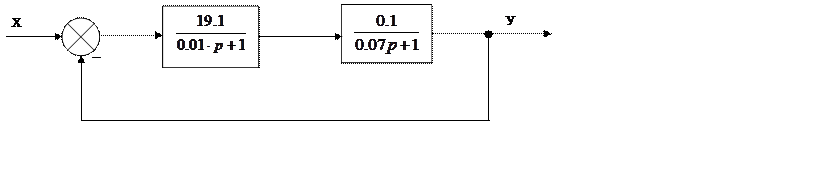
                                                                                                     Структурная схема САУ

Введем передаточные функции элементов с помощью функции tf:

w1=tf([19.1],[0.01 1])  

 Transfer function:

   19.1

----------

0.01 s + 1  

w2=tf([0.1],[0.07 1])  

 Transfer function:

   0.1

----------

0.07 s + 1

Передаточная функция разомкнутой системы будет:

Wp=w1*w2  

 Transfer function:

         1.91

-----------------------

0.0007 s^2 + 0.08 s + 1   

 

          Функция zpk позволяет определить нули, полюса и коэффициент усиления системы:

Wp=zpk(Wp)  

 Zero/pole/gain:

    2728.5714

-----------------

(s+100) (s+14.29)   

nд.

nд.

Можно заключить, что разомкнутая система имеет статический коэффициент усиления k=1.91, и состоит из двух апериодических звеньев, с частотами среза: ω_ср1=14.29 рад/с; ω_ср2=100 рад/с.

K=20*log10(1.91)  

K =

    5.6207   

Передаточная функция замкнутой системы будет:

Wz=tf(Wp/(1+Wp))  

Transfer function:

           2729 s^2 + 3.118e005 s + 3.898e006

---------------------------------------------------------

s^4 + 228.6 s^3 + 1.865e004 s^2 + 6.384e005 s + 5.939e006

          Для вызова графического интерфейса служит функция ltiview, отрывающая          специальное средство просмотра временных и частотных характеристик модели – LTI-viewer (LTI systems – Linear Time Invariant Systems линейные, инвариантные во времени системы, в отечественной литературе называют линейными стационарными системами).

ltiview  

Окно интерактивного обозревателя

Интерактивный обозреватель взаимодействует с собственной рабочей средой, которая формируется независимо от рабочей среды MATLAB. Поэтому в случай вызова рассматривамой функции без задания аргументов исследуемую модель необходимо поместить в рабочую среду обозревателя.

Для обмена данными между рабочими средами MATLAB и LTI-viewer используются команды меню окна обозревателя File/Import, открывающее диалоговое окно:

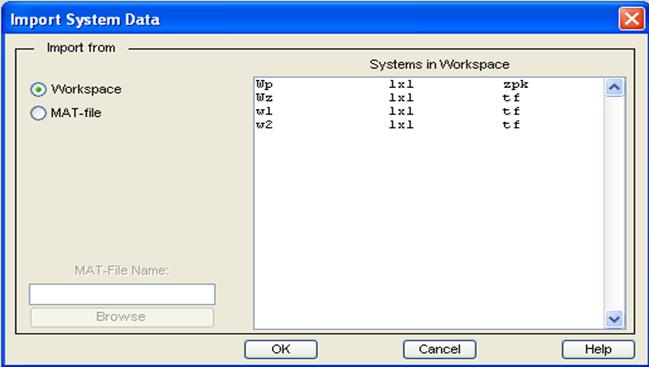
Окно загрузки модели

В окне представлены имена моделей, количество их входов и выходов, а также тип. После выбора системы окно загрузки закроется, а в окне обозревателя отразиться график переходного процесса модели (Step).

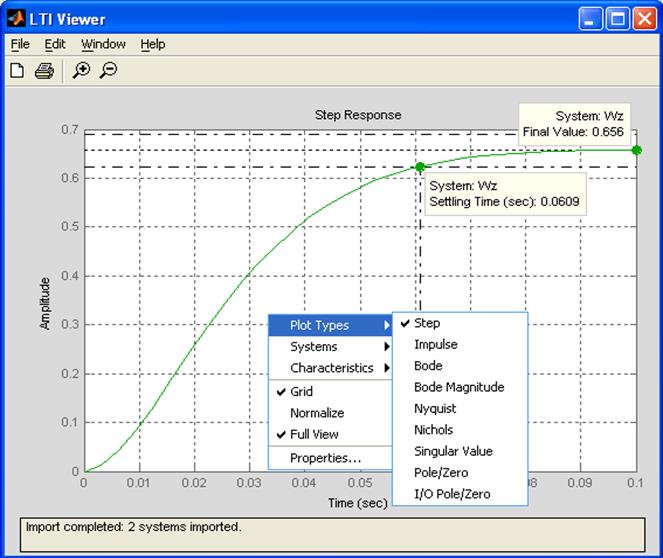
Переходный процесс в замкнутой системе

Если теперь указатель мыши подвести к произвольной точке данного графика и нажать левую кнопку, то появиться всплывающее сообщение об имени системы, величинах абсциссы и ординаты графика. Щелчок правой кнопкой мыши в области графика приведет к появлению контекстного меню, позволяющего выбирать тип графика, отображаемые системы, а также различные характеристики (время переходного процесса,  установившееся значение, перерегулирование и т. д.)

Таким образом, можно получить ЛАЧХ, ЛФЧХ (Bode) и АФЧХ (Nyquist) разомкнутой системы и определить по графикам запасы устойчивости:

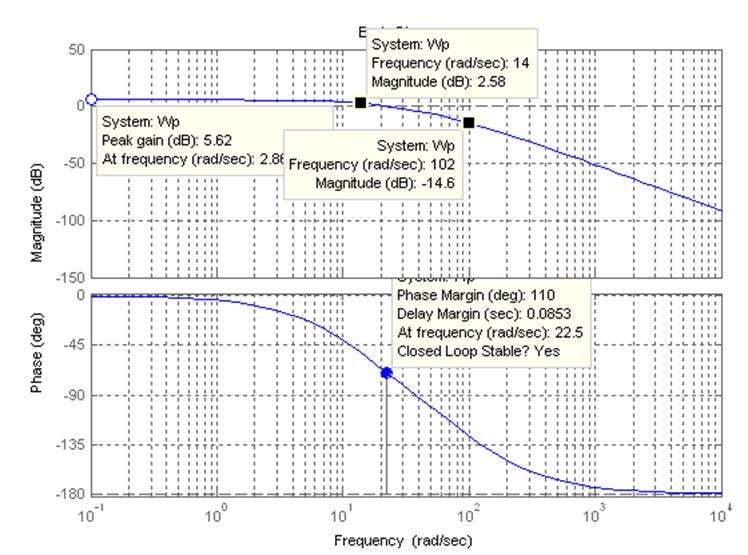
           ЛАЧХ и ЛФЧХ разомкнутой системы

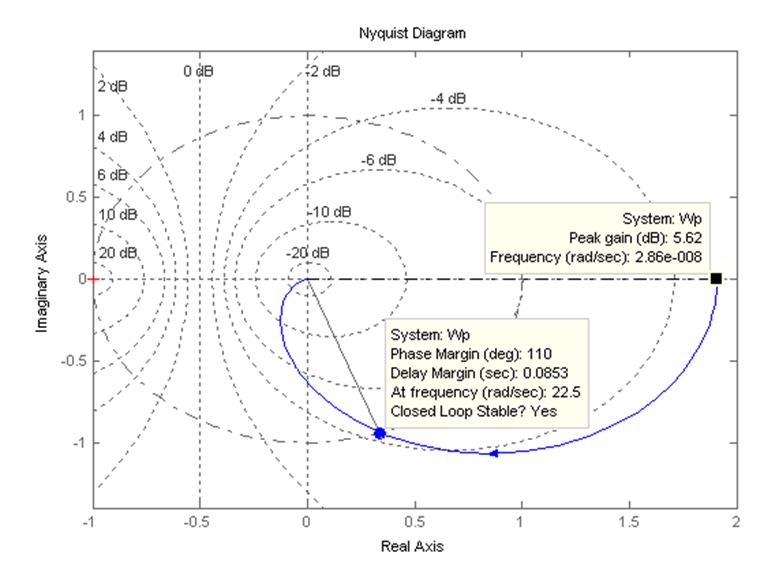
        АФЧХ разомкнутой системы

Перейдем от непрерывной модели к дискретной с интервалом дискретизации Ts, используя экстраполятор нулевого порядка ('zoh'), для этого служит команда с2d.

Ts=0.001;Wdp=tf(c2d(Wp,Ts,'zoh'))  

Transfer function:

0.001314 z + 0.001265

---------------------

z^2 - 1.891 z + 0.892

Sampling time: 0.0011

Для проверки качества выполненной аппроксимации сравним частотные характеристики исходной непрерывной и полученной дискретной модели. Из графика следует, что аппроксимация выполнена верно.

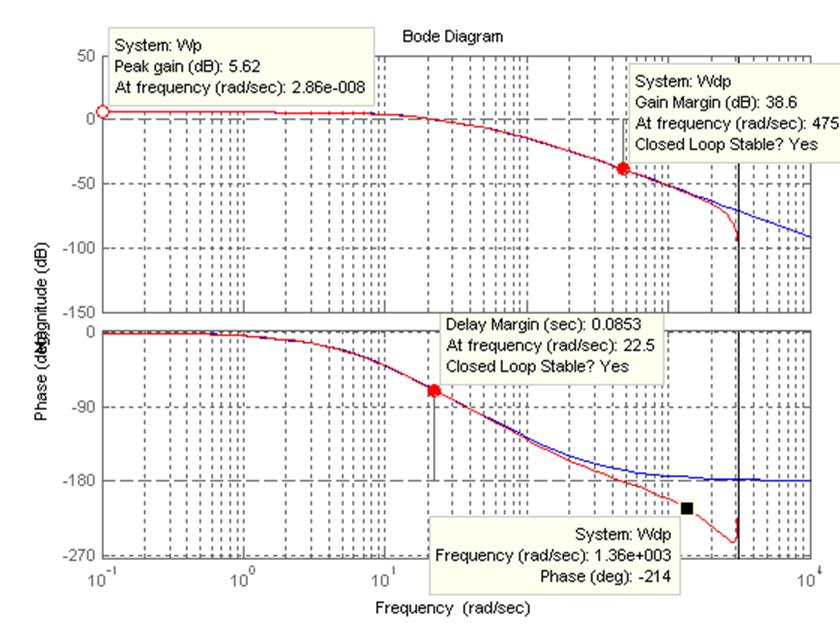
Частотные характеристики исходной непрерывной и полученной дискретной модели

Также построим переходный процесс в замкнутой дискретной системе, для этого определим ее передаточную функцию.