Применение пакета Сontrol System Toolbox, входящего в программу MATLAB, страница 2

Wdz=Wdp/(1+Wdp)  

Transfer function:

0.001314 z^3 - 0.001219 z^2 - 0.001219 z + 0.001128

---------------------------------------------------

   z^4 - 3.78 z^3 + 5.357 z^2 - 3.374 z + 0.7968

Sampling time: 0.001  

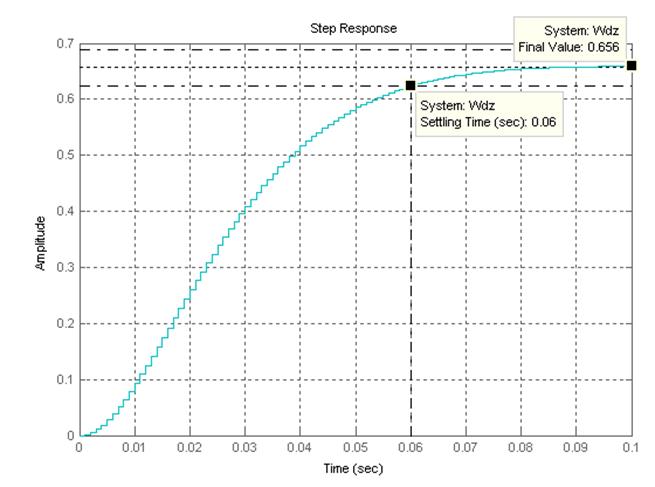
Переходный процесс в замкнутой дискретной системе

Допустим, требуется уменьшить время переходного процесса, тогда необходимо рассчитать цифровой регулятор, который будет осуществлять коррекцию. Проектирование корректирующего устройства можно провести методом корневого годографа, соответсвующий графический интерфейс открывает команда sisotool.

sisotool  

 

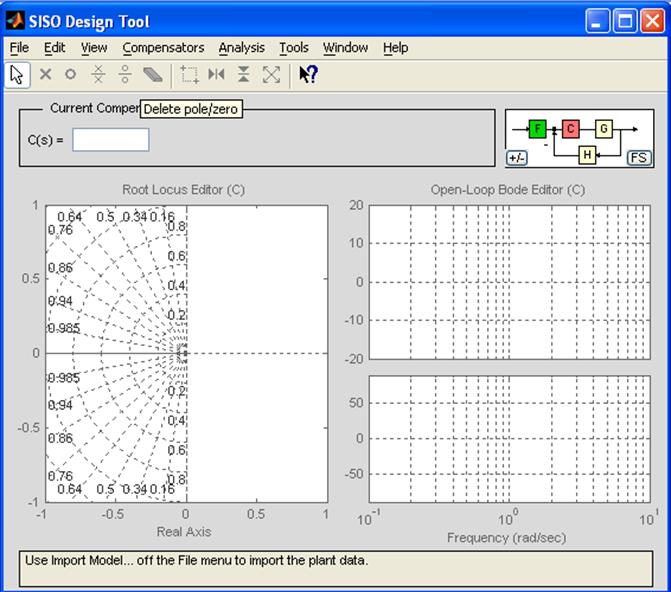
Графический интерфейс sisotool

В меню интерфейса команда File/Import открывает диалоговое окно загрузки моделей и задания структуры системы.

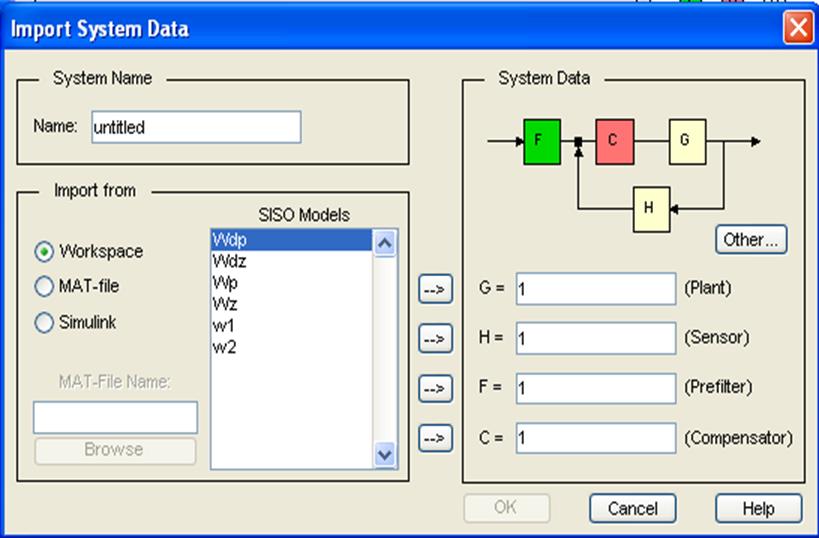
Диалоговое окно загрузки моделей и задания структуры системы

В верхнем левом углу окна загрузки приведена структурная схема замкнутой системы. В ней F, C, G, H – звенья, модели которых можно загружать из рабочей среды MATLAB, из mat-файла или из среды Simulink. Звено, обозначенное буквой С, - это компенсирующее динамическое звено, структуру и параметры которого нужно определить. Загрузка моделей осуществляется кнопкой -->. После загрузки дискретной системы получим.

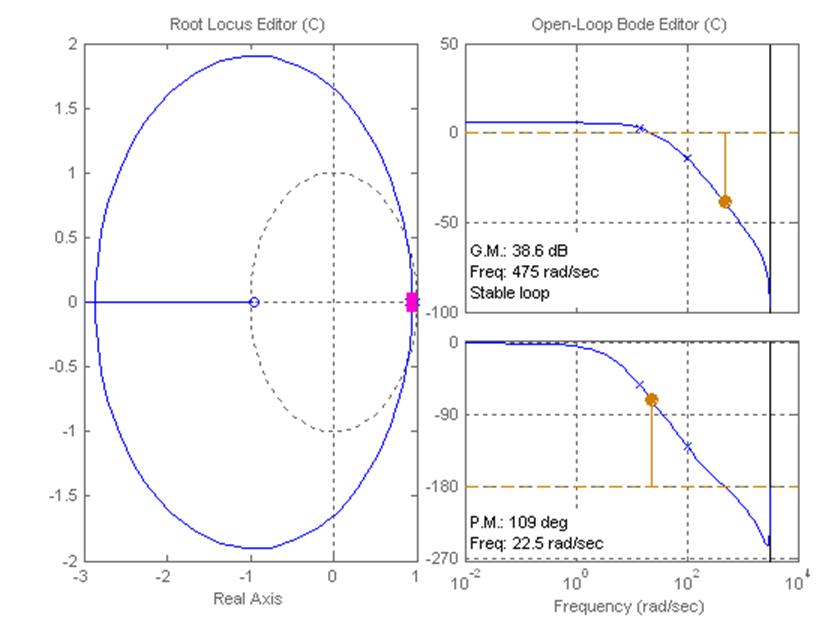
Корневой годограф и логарифмические частотные характеристики исследуемой системы

На графике первой характеристики на комплексной плоскости нулей  полюсов отображены полюсы замкнутой системы (квадратиками), ее нули (кружочками) и линии их перемещения при изменении коэффициента усиления компенсатора.

Из корневого годографа следует, что с увеличением коэффициента усиления полюсы замкнутой системы быстро выходят за пределы единичной окружности и система становится неустойчивой. Поэтому введем динамическую коррекцию в виде дискретного  компенсатора с передаточной функцией:

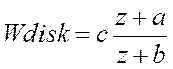
Добавим один полюс и один ноль с помощью кнопок с обозначением крестика и кружочка, расположенных над графическим окном слева. Кроме того, при заданной структуре компенсатора нули и полюса  можно передвигать непосредственно на графике при помощи мыши; при этом соответственно измениться значение коэффициента усиления компенсатора в поле Gain.

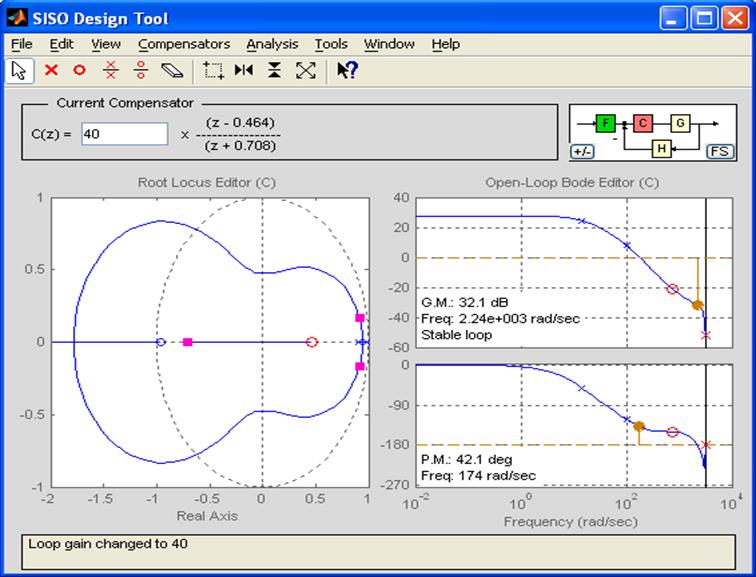
Корневой годограф скорректированной системы

Просмотреть график переходного процесса в скорректированной системе можно с помощью меню Analysis/Response to Step Command, которое запускает интерактивный обозреватель LTI-viewer

Таким образом, руководствуясь графиком переходного процесса и соответственно прямыми показателями качества системы, подберем коэффициенты a, b и c.  a= - 0.464  b= 0.708  c= 40

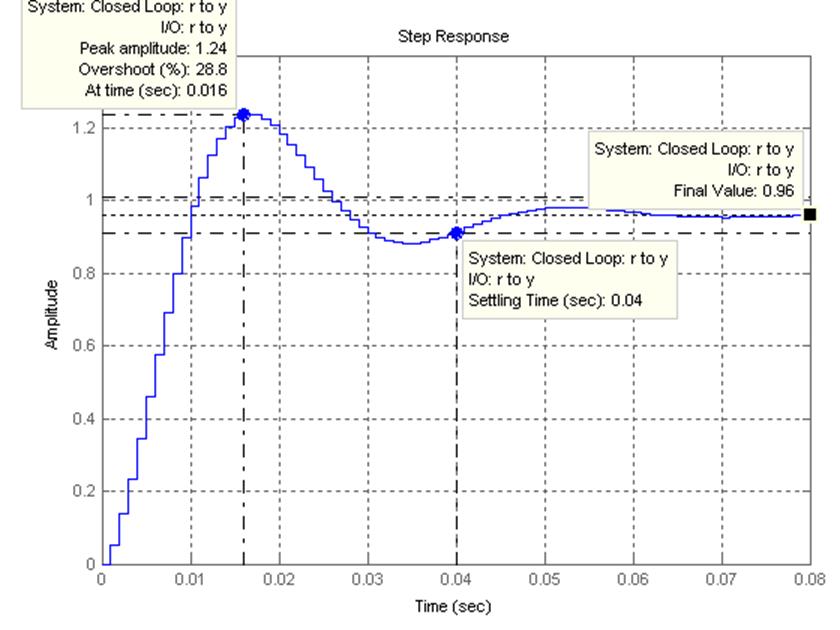
Переходный процесс в скорректированной системе

То есть путем введения компенсатора с передаточной функцией 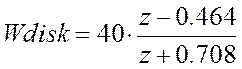 удалось уменьшить время регулирования.

Дискретный компенсатор реализуется в виде цифрового фильтра, передаточная функция которого:

.

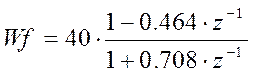Но передаточной функции 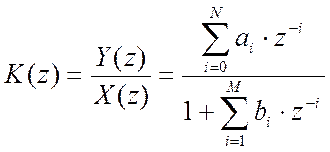           ,                                                                      соответствует разностное уравнение  .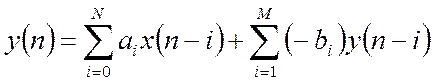          

И если перейти от передаточной функции к разностному уравнению, то можно исследовать реакцию звена на различные входные воздействия.

Для перехода к разностному уравнению дискретного компенсатора воспользуемся функцией filter.

Определим реакцию компенсатора на единичное входное воздействие, тогда сигнал x на входе будет изменяться по закону:

x=[0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1]  

x =

  Columns 1 through 13

     0     1     1     1     1     1     1     1     1     1     1     1     1

  Columns 14 through 17

     1     1     1     1  

              Выходной сигнал у будет изменяться по закону:

y=40*filter([1 -0.464],[1 0.708],x)  

y =

  Columns 1 through 8

         0   40.0000   -6.8800   26.3110    2.8118   19.4493    7.6699   16.0097

  Columns 9 through 16

   10.1051   14.2856   11.3258   13.4213   11.9377   12.9881   12.2444   12.7709

  Column 17

   12.3982  

plot(y);grid  

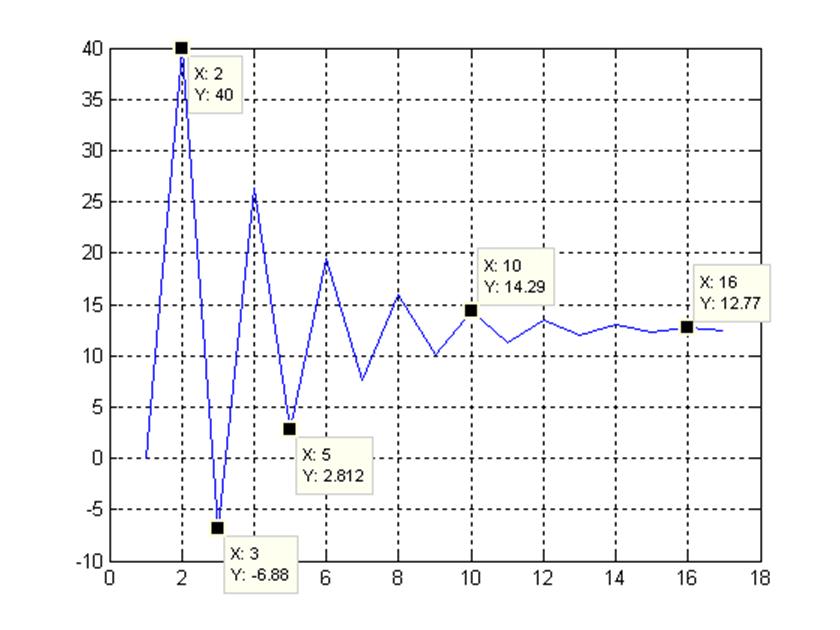
          Реакция компенсатора на единичное входное воздействие

          При этом передаточная функция дискретного компенсатора:

Wdisk=zpk([0.464],[-0.708],[40],Ts)  

Zero/pole/gain:

40 (z-0.464)

------------

 (z+0.708)

Sampling time: 0.001  

ltiview  

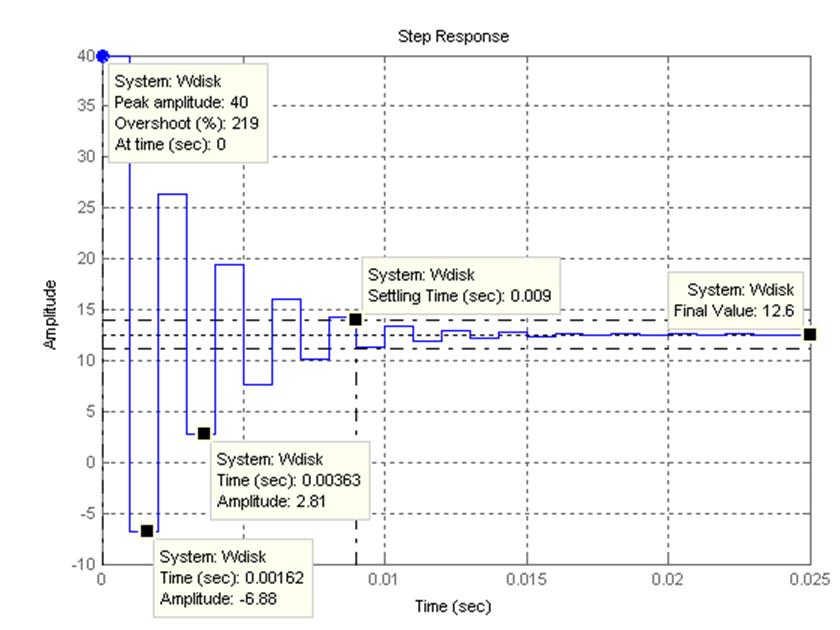
          Переходный процесс в дискретном компенсаторе

Сравнивая график переходного процесса и реакцию компенсатора, рассчитанную из разностного уравнения можно сделать вывод, что реализация   цифрового фильтра выполнена верно.

Заключение:

Применение пакета Сontrol System Toolbox, входящего в программу MATLAB, позволяет провести полный цикл исследования и проектирования  систем автоматического управления и регулирования, начиная от задания передаточных функций звеньев непрерывной части и заканчивая реализацией разностного уравнения для разработанного цифрового корректирующего устройства. Кроме того, применение данного пакета  освобождает разработчика от выполнения сложных математических вычислений, что позволяет заниматься только творческой частью работы  и соответственно значительно ускорить проектирования систем.

Дьяконов В. П. MATLAB 6/6.1/6.5+Simulink 4/5 в математике и моделировании. Полное руководство пользователя. М.: СОЛОН-Пресс, 2003.