Исследование механизированной поточной линии производства обыкновенной шоколадной массы большой производительности, страница 5

Создадим матрицу для решения дифференциального уравнения.

Зададим матрицы для трех начальных условий:

             

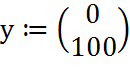
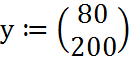
Возьмем количество точек равным 1000 и конечное время интегрирования 200, то матрица решений запишется как:

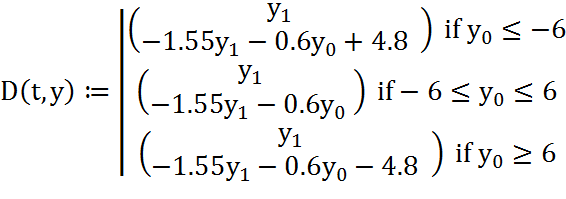                                         (57)

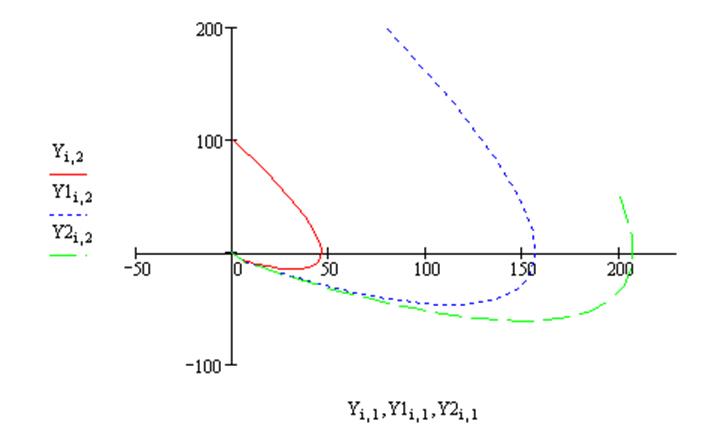
Построим фазовый портрет:

                                                                                                

 

                                                                            

 

Рисунок 13 - Фазовый портрет нелинейной системы

  

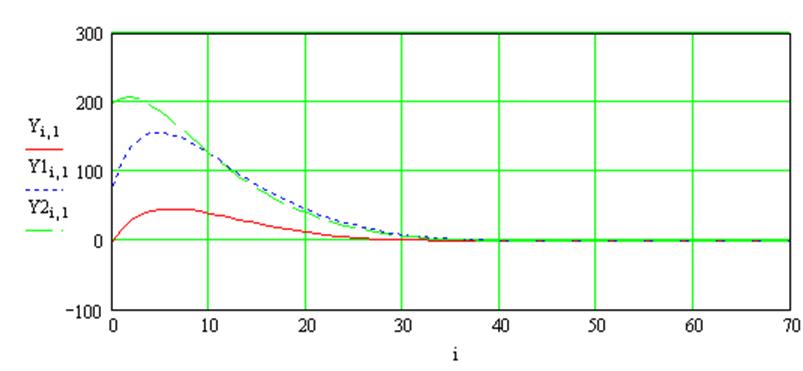
Рисунок 14 - Переходный процесс нелинейной системы

3.3 Вывод по исследованию нелинейной системы

На участке 0 – 1 координата  x  растет, а координата ν уменьшается. В точке 1 координата  x  достигает максимального значения.

На участке 1 – 2 координата  x  уменьшается. В точке 2 координата ν принимает значение, равное 0.

На участке 0` – 1` координата  x  растет, а координата ν уменьшается. В точке 1` координата  x  достигает максимального значения.

На участке 1` – 2` координата  x  уменьшается. В точке 2` координата ν принимает значение, равное 0.

На участке 0`` – 1`` координата  x  растет, а координата ν уменьшается. В точке 1`` координата  x  достигает максимального значения.

На участке 1`` – 2`` координата  x  уменьшается. В точке 2`` координата ν принимает значение, равное 0.

Характер фазового портрета таков, что фазовые траектории приближаются к нулю. Следовательно, можно сделать вывод, что система устойчива.

4 ИССЛЕДОВАНИЕ ДИСКРЕТНОЙ СИСТЕМЫ

4.1 Z-преобразование

 

Рисунок 15 - Упрощенная схема дискретной системы

Введём вынужденную обратную связь:

Рисунок 16 - Итоговое преобразование дискретной САУ

Передаточная функция непрерывной части системы:

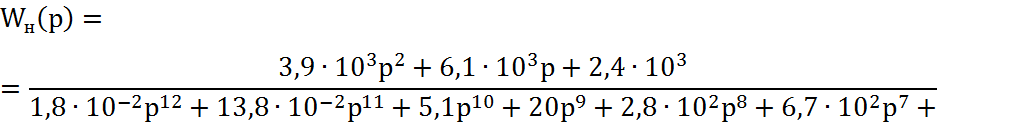
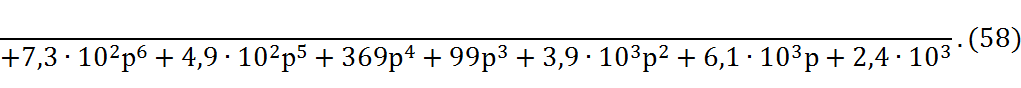
Передаточная функция дискретной части системы:

где Т = 0,06 – период дискретизации (шаг квантования)

Примем обозначение   е^-Тр=z, получим:

Находим изображение переходной характеристики

и разлагаем ее на простые дроби:

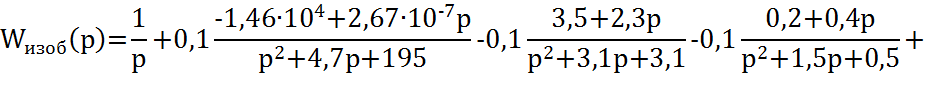
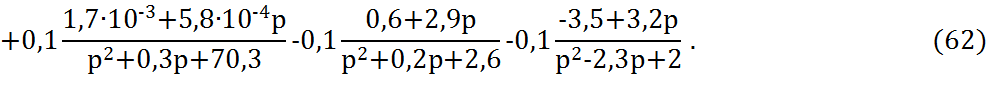
Находим обратное преобразование Лапласа:

Из временной функции получим импульсную и найдем Z-преобразование.

Введём замену t=n·T:

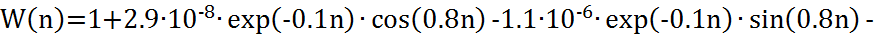
где Т = 0,06 – период дискретизации (шаг квантования).

          Z-преобразованная передаточная функция непрерывной части будет иметь вид:

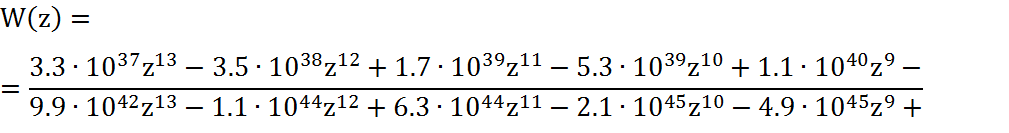
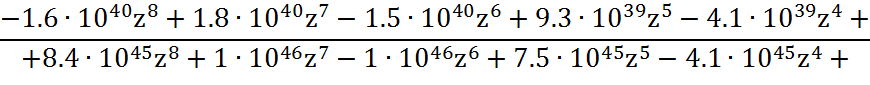
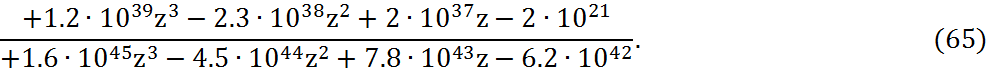
Заменим дискретную часть Z-преобразованной и получим передаточную функцию дискретной системы:

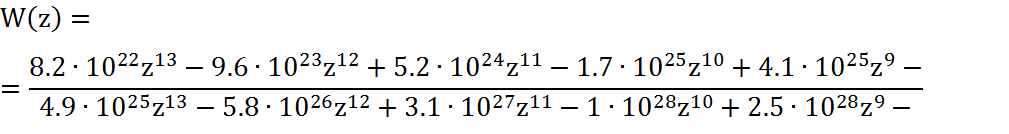
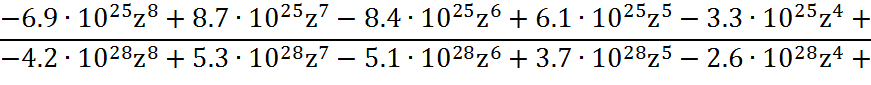
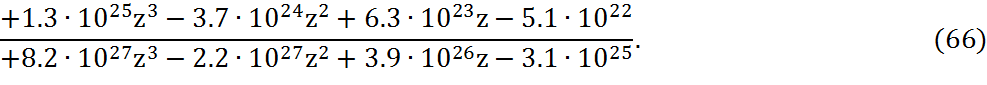
4.2  Устойчивость по критерию Шур-Кона

Определим устойчивость системы по критерию Шур-Кона с помощью Matchad.

В соответствии с критерием Шур-Кона система будет устойчивой, если определители  для чётных k и определители  для нечётных k.

Определители Шур-Кона составляются из коэффициентов характеристического уравнения.

Характеристическое уравнение системы имеет вид:

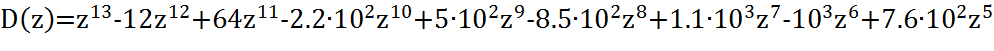
Выпишем коэффициенты характеристического уравнения:

a₁=-12, a₂=64, a₃=-2.2, a₄=5·10², a₅=-8.5·10², a₆=1.1·10³, a₇=-10³, a₈=7.6·10²,

a₉=-4.2·10², a₁₀=1.7·10², a₁₁=-46, a₁₂=7.9, a₁₃=-0.6.

Составим определители:

 

 

 

 

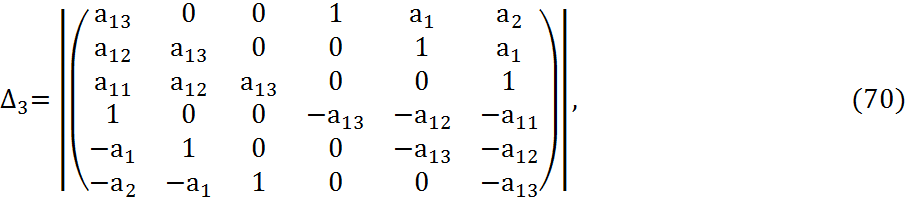
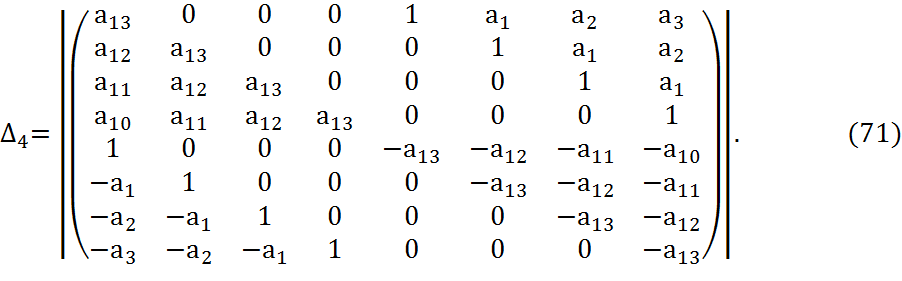
Посчитаем данные определители с помощью Matchad:

∆₁=-0.64,

∆₂=-0.08,

∆₃=0.064,

∆₄=1395.

Видно что при чётных k - , а при нечётных k - , следовательно, система не устойчива.

4.3 Переходный процесс дискретной системы

Используя математический редактор MathCAD, построим переходный процесс системы:

h(n)=8.73*10^-5j(2.87-0.631j)ⁿ+1.15*10^-4(1+1.43*10^-17j)ⁿ-1.64*10^-4(0.788-.394j)ⁿ  (72)

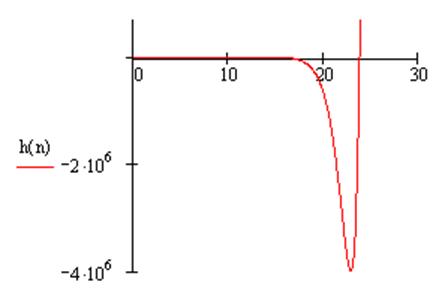
Рисунок 17- График переходного процесса дискретной системы

4.4 Билинейное преобразование