Для устойчивой системы необходимо и достаточно, чтобы годограф Михайлова при изменении частоты от нуля до бесконечности повернулся против часовой стрелки, начиная с вещественной оси, на число квадрантов равное порядку характеристического уравнения (3), последовательно проходя эти квадранты.
Заменим в уравнении (3) ![]() :
:
L(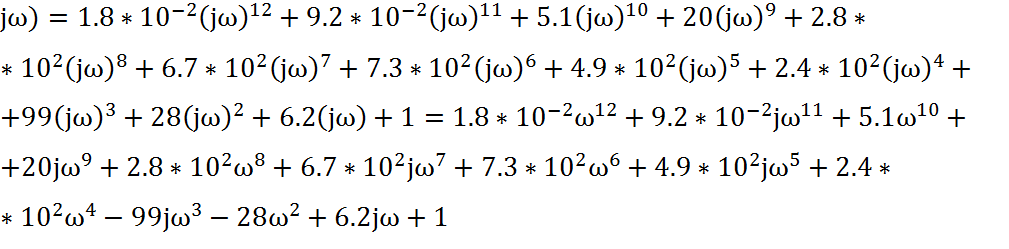 . (13)
. (13)
Выделим вещественную и мнимую части:
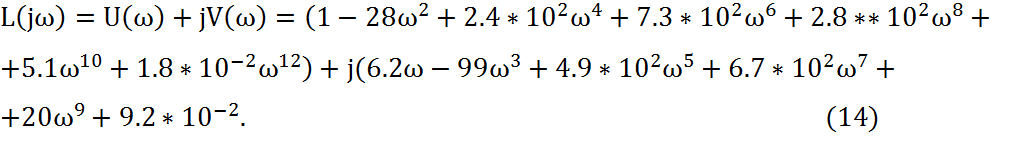
Таблица 2-Значения![]() и
и ![]() при
изменении
при
изменении ![]() от 0 до 1.2
от 0 до 1.2
|
№ |
|
|
|
|
1 |
0 |
1 |
0 |
|
2 |
0.2 |
0.311 |
0.613 |
|
3 |
0.4 |
5.838 |
2.265 |
|
4 |
0.6 |
60.817 |
39.396 |
|
5 |
0.8 |
320.274 |
258.037 |
|
6 |
1 |
1.228*103 |
1.087*103 |
|
7 |
1.2 |
3.874*103 |
3.56*103 |
![]()
![]()
![]()
![]()

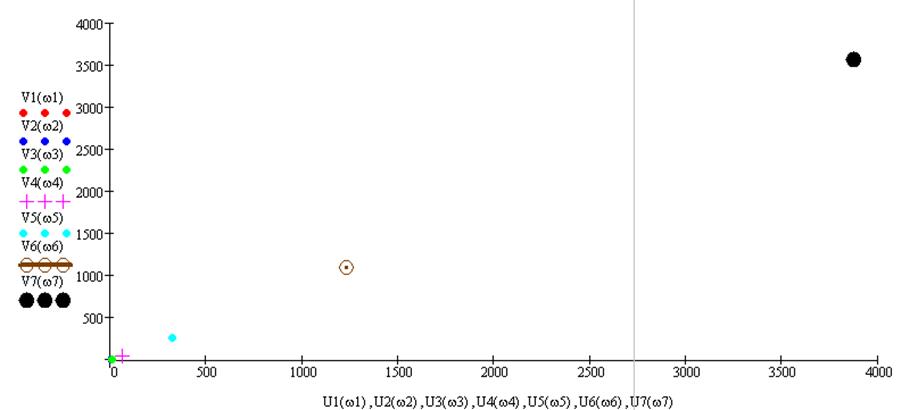
Рисунок 4 - Годограф Михайлова
Система не устойчива, так как вектор не обходит последовательно n-квадрантов.
2.4 Определение устойчивости САУ по критерию Евсюкова
Определим величины k:
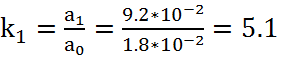 ,
(15)
,
(15)
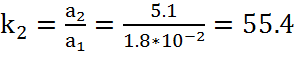 ,
(16)
,
(16)
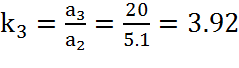 , (17)
, (17)
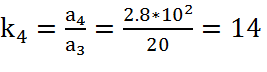 ,
(18)
,
(18)
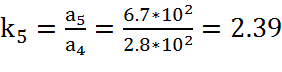 ,
(19)
,
(19)
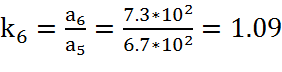 ,
(20)
,
(20)
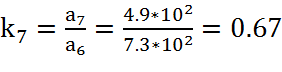 ,
(21)
,
(21)
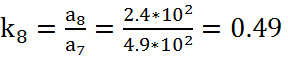 ,
(22)
,
(22)
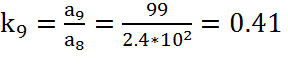 ,
(23)
,
(23)
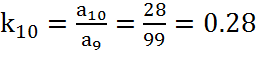 ,
(24)
,
(24)
 ,
(25)
,
(25)
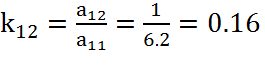 .
(26)
.
(26)
Определим величины n:
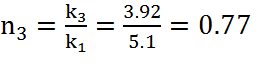 ,
(27)
,
(27)
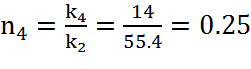 , (28)
, (28)
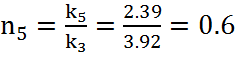 ,
(29)
,
(29)
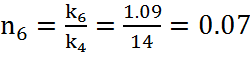 ,
(30)
,
(30)
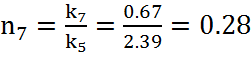 ,
(31)
,
(31)
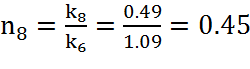 ,
(32)
,
(32)
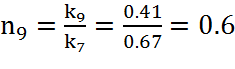 ,
(33)
,
(33)
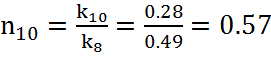 ,
(34)
,
(34)
 ,
(35)
,
(35)
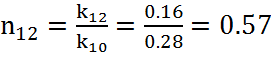 ,
(36)
,
(36)


Условия (38) не выполняются, следовательно, система не устойчива. Приведем систему к устойчивому состоянию. Для этого уменьшим коэффициенты n3, n9, n10, n12 в 1,5 раза и получим значение n3 = 0.51, n9=0.4, n10 =0.38, n12 =0.38. Условие (38) выполняется, система устойчива.
Для получения устойчивой системы коэффициенты n3, n9, n10, n12 были
уменьшены в 1,5 раза, значит необходимо увеличить коэффициент k1
, k9 , k10 , k12 в 1,5 раза, согласно формулам (27),(33)-(34),(36).Тогда k1=7.68, k9=0.268, k10 =0.186, k12=0.07. Для того, чтобы система стала устойчивой
необходимо в характеристическом уравнении изменить значение коэффициентов а1,
а8, а10, а11,
которые согласно формулам (15),
(23)-(24), (26) примут следующие значения:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.