Исследование механизированной поточной линии производства обыкновенной шоколадной массы большой производительности, страница 4

а₁=13,82*10^-2, а₈=369, а₁₀=18.4, а₁₁=14,3.

Передаточная функция САУ примет вид:

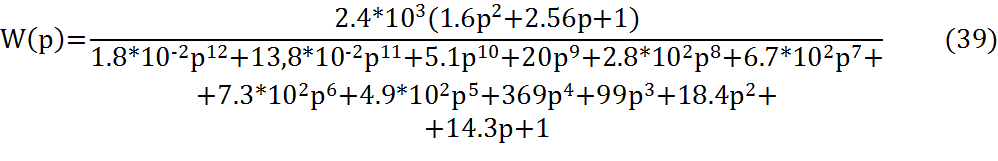
2.5 Переходный процесс системы и определение показателей качества

Используя математический редактор MathCAD, построим переходный процесс системы.

h(t)=2.37*10³+2.94*10^-8exp(-2.36t)cos(13.8t)-1.18*10⁶exp(-2.36t)*

*sin(13.8t)                                                                                                                    (40)

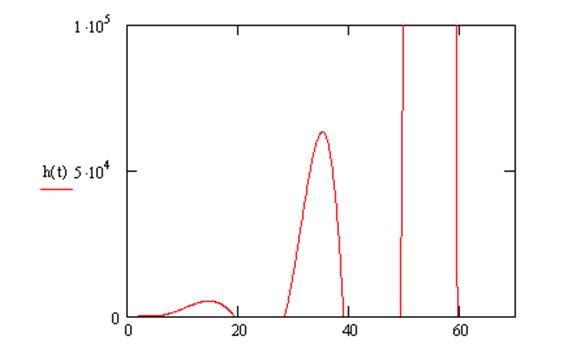
Рисунок 5 - Переходный процесс системы

2.6 АЧХ системы и определение показателей качества

Используя математический редактор MathCAD, построим амплитудно-частотную характеристику системы.

Заменим в уравнении (39) :

(41)

 

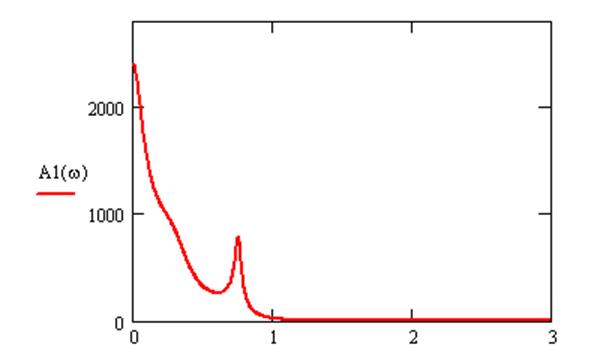
Рисунок 6 - Амплитудно–частотная характеристика системы

Определение показателей качества:

А₀ = 2400;

А_max = 2400;

показатель колебательности ;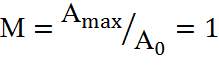

полоса пропускания 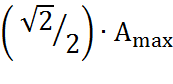 = 1697          .

2.7 ЛАЧХ системы и определение запасов устойчивости

Используя математический редактор MATLAB, построим ЛАЧХ и ЛФЧХ системы.

Рисунок 7 - ЛАЧХ системы

      2.8 Аппроксимация ЛАЧХ и определение передаточной функции

 

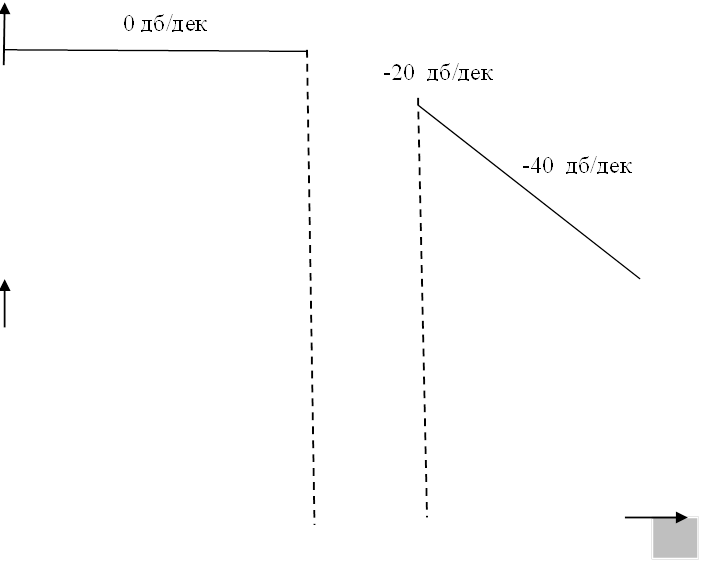
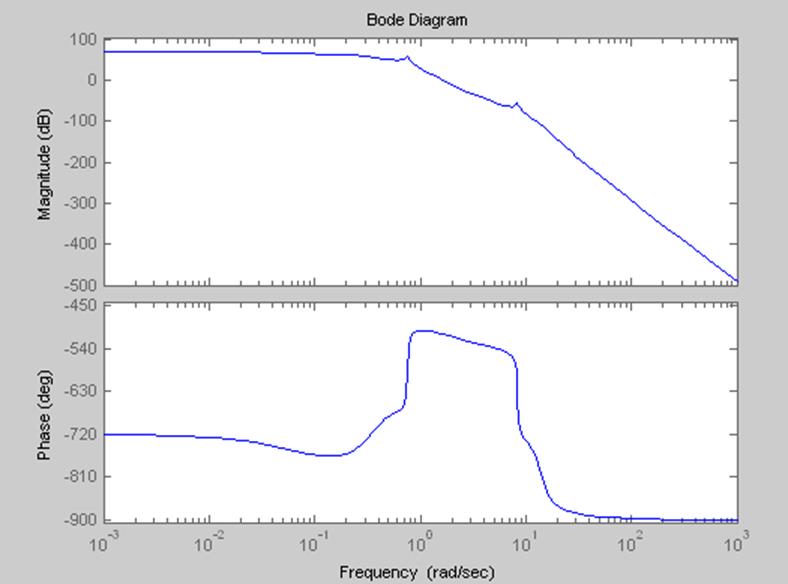
Рисунок 8-Аппроксимация ЛАЧХ системы

Передаточная функция аппроксимированной ЛАЧХ имеет вид:

 ,                                                                (43)

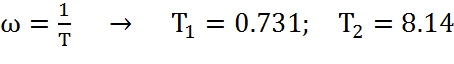.                                                      (44)

С учетом коэффициентов выражение (42) примет вид:

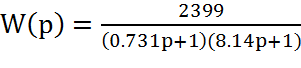.                                                                              (45)

2.9 Вывод по исследованию линейной системы

В ходе исследования линейной системы была получена передаточная функция системы. Определили, что система является неустойчивой по критериям устойчивости Гурвица, Михайлова и Евсюкова. Благодаря критерию устойчивости Евсюкова система была приведена к устойчивому состоянию. Построили переходный процесс и АЧХ системы, определили показатели качества. При помощи математического редактора MATLAB построили ЛАЧХ системы и определили запасы устойчивости.

3 ИССЛЕДОВАНИЕ НЕЛИНЕЙНЫХ СИСТЕМ

3.1 Преобразование системы

 

 

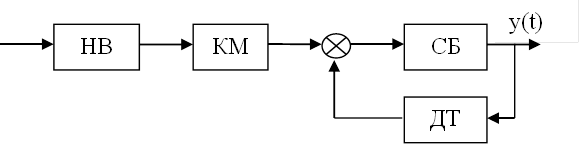Рисунок 9 - Функциональная схема САУ с нелинейным элементом

         График, описывающий нелинейный элемент  приведен на рисунке 10.

 

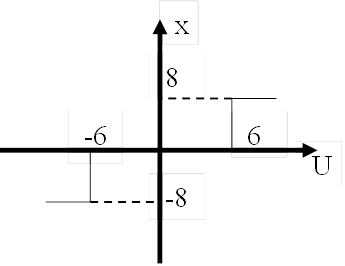Рисунок 10 - Релейная статическая характеристика

Применяя правила преобразования структурных схем, упростим схему, изображенную на рисунке 9:

                                                                                                       

Рисунок 11 - Упрощенная схема нелинейной системы

Введем вынужденную обратную связь:

 

                                        -

Рисунок 12 - Итоговое преобразование САУ с нелинейным элементом

С учетом всех преобразований W_общ (p) примет вид:

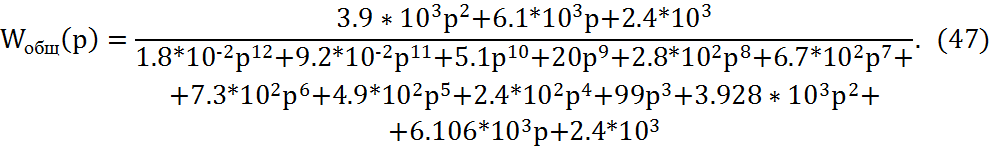
3.2 Построение фазового портрета

 Передаточная функция есть 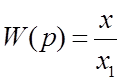или ,                     (48)

где  W(p)-передаточная функция линейной системы;

Подставляя в формулу (48) значение передаточной функции получим:

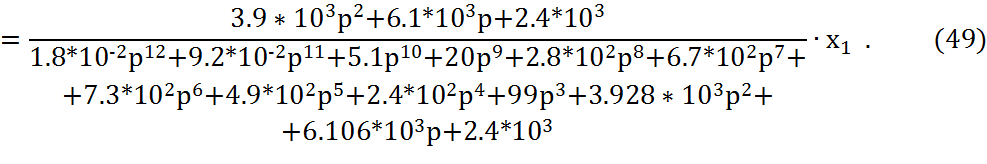
Степени больше второй оказывают небольшое влияние на систему в целом, поэтому мы можем ими пренебречь.

Приведенную формулу можно записать в виде:

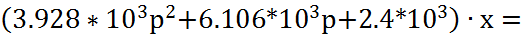
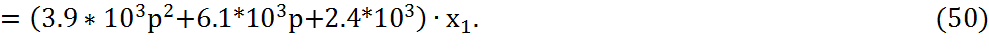
Введем замену 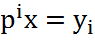 и :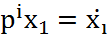

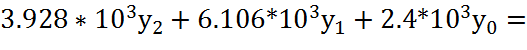
Исключим из правой части уравнения производную, получим:

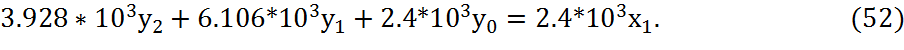
Перенесем у₂ влево:

 

Так как в качестве нелинейного элемента используется реле с однозначной статической характеристикой с зоной нечувствительности, то подставляя значение  для трех участков, получим систему уравнений:

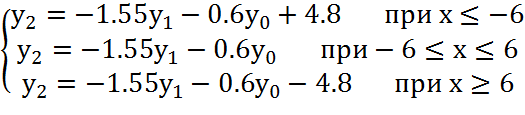                                               (54)