Расчет основных параметров ветротепловой установки (Глава 2 магистерской работы), страница 6

Расчет передаточного отношения:

                                                        

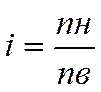
,где  nн – номинальная частота вращения насоса НС;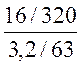

      nв – частота вращения ветрового колеса.

Подставляя численные данные, получаем:   i= 28,08  

Исходя из рассчитанной величины передаточного отношения               i= 28,08.  Выбираем из справочной литературы ([20] стр. 24) тип и конструкцию мультипликатора. Остановим свой выбор на  планетарном мультипликаторе типа 3К с двухвенцовым сателлитом,  т. к. данная конструкция полностью удовлетворяет по условию     i= 28,08. Также данный тип планетарного редуктора обладает довольно высоким КПД, широко  распространен, имеет малый вес и малые габаритные размеры. Кинематическая схема предоставлена на рис. 2.4.

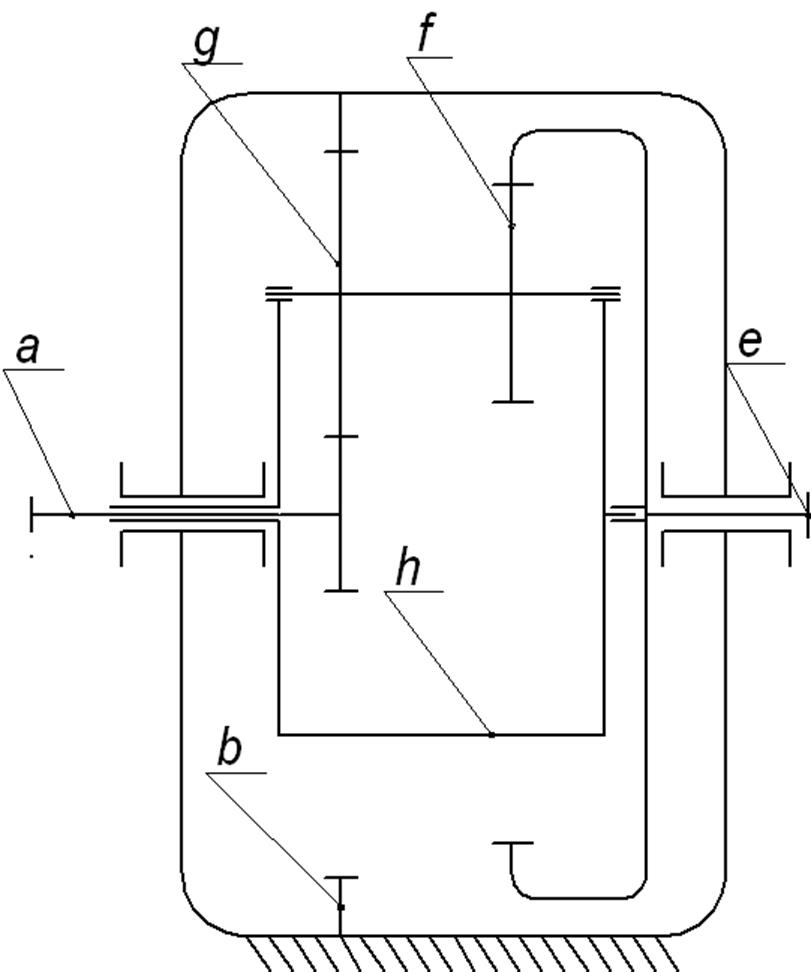
Рис. 2.4   Схема выбранного планетарного редуктора 3К с двухвенцовым сателлитом.(a,f,b,e,h,g – обозначение шестерней)

Определение основных параметров планетарного  редуктора

Для передачи типа 3К  с  n_w = 3  и  z_a, z_b, z_e – (количествам зубьев) кратным трем. Из справочной литературы ([19] стр. 209 таб. 2.5) можно определить число зубьев зубчатых колес по заданной величине передаточного отношения  i= 28,08  

Получаем следующие значения:

i=28,44 - уточненное передаточное отношение;

z_a = 18;   z_b = 114;    z_e = 96;    z_g = 48;    z_f = 30 – количество зубцов в зубчатых передачах. Данное количество зубьев справедливо для передачи с зубчатым колесом одного модуля  -  m_a = m_b = m_e .

Определение КПД передачи  3К с цилиндрическими колесами при учете потерь на трение производится по следующей формуле ([20] стр. 196):

                                            

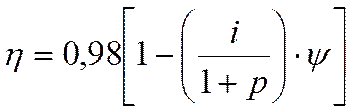
   где    i = 28 – передаточное отношение;

            р= 6,3 - шаг  равный:                                     ;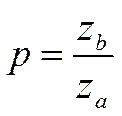

           ψ = 0,011 – коэффициент потерь в зацеплениях с центральными сателлитами.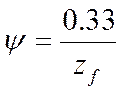                                                         

Расчет основных геометрических размеров сводится к вычислению делительного межосевого расстояния исходя из, которого можно рассчитать  все остальные  необходимые размеры планетарного мультипликатора. Расчет проводится по формуле:

                            

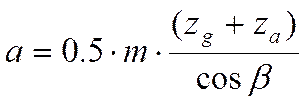
где              m = 5 мм – модуль выбираем из таблицы [19] стр. 49;

                    β = 0 – угол наклона зуба на делительном цилиндре.

Подставляя численные значения  вычисляем  a= 165 мм. Так как у нас передача с высокой коррекцией то a=a_ω

a_ω– межосевое расстояние в зубчатой паре   a_ω  = 165 мм

Определение делительных диаметров цилиндрических колес

Определение делительных диаметров цилиндрических колес проводятся по формулам [20] стр. 54:

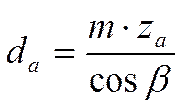
где     m – расчетный модуль;

       z_a – количество зубьув на шестерни а

        β = 0 – угол наклона зубьев.

Подставляя численные значения получаем d_a = 90 мм.

Остальные диаметры шестеренок вычисляются аналогично и имеют вид:

      d_g =240 мм       d_f =150 мм      d_b=570мм      d_e =480 мм

Вычисляем начальный диаметр воспользовавшись формулой [20] стр. 55:

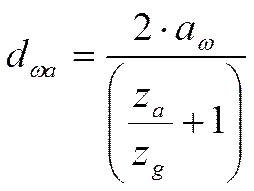
где    z_a, z_g – количество зубьев на aиgшестернях

Подставляя свои численные данные получаем:

d_ωa = 92 мм;d_ωg = 238 мм;   d_ωb = 570 мм;    d_ωе = 483 мм;     d_{ωf =} 143 мм.              

Определение рабочей ширины зуба.

Вычисление рабояей ширины зуба проводится по формуле [19] стр. 125:

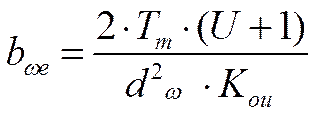
где       Т_м – крутящий момент на шестерне;

             К_оu =0,64 кгс/мм² – коэффициент учитывающий массу материала;

             U – передаточное число;

             d_ω – нормальный диаметр;

Крутящий момент на шестерне равен:

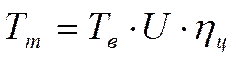
где      Т_в – крутящий момент на валу мультипликатора:

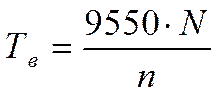
где        N = 10 кВт – мощность установки;

              n = 53,4 об/мин – частота оборотов;

Вычисляя получим Т_в = 1788 Нм

U = z_e/z_f  - передаточное число  данного зубчатого зацепления U =3,2

η_ц = 0,97 – КПД цилиндрической передачи.

Подставляя свои численные данные получаем:  b_ωe = 30 мм. Остальные рабочие ширины зубьев подбирают аналогично ориентируясь на вычисленную ранее ширину: