Для
коэффициента подъемной силы , полученного в опыте при угле атаки δ' и
отношении L/d, значения ζω и δ (в градусах) (соответствующие ![]() =
=![]() ) получаются из формул:
) получаются из формул:
ζω = ζω '-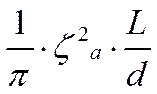 ;
;
δ = δ' - 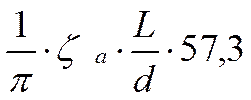 .
.
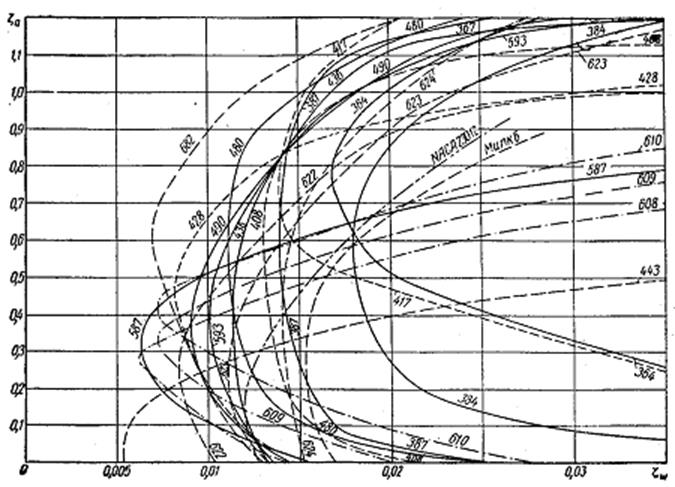
Рис. 2.9 Поляры профилей приведенных на рис. 2.10.
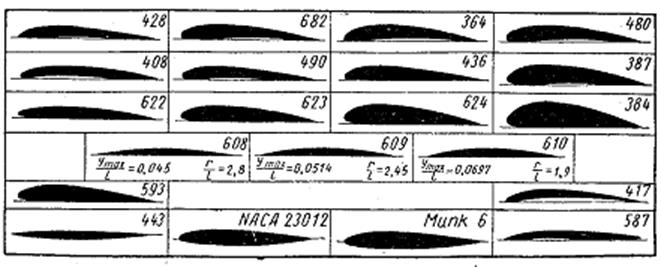
Рис. 2.10 Формы профилей характеристики которых приведены на рис. 2.9
На рис. 2.9 даны кривые пересчитанных значений ζa и ζω для некоторых форм профилей, которые показаны на рис. 2.10. Эти данные были взяты из опубликованных работ Аэродинамического исследовательского института в Геттингене . Проанализировав все выше перечисленное, выбираем профиль номер 384. Размер профиля дан в табл. 2.1 в виде процентов от длины L.
Таблица 2.1
|
x |
0 |
1.25 |
2.5 |
5.0 |
7.5 |
10 |
15 |
20 |
|
y0 |
4.15 |
7.25 |
8.95 |
11.45 |
13.40 |
14.95 |
17.15 |
18.55 |
|
yu |
4.15 |
2.25 |
1.55 |
1.10 |
0.80 |
0.85 |
0.30 |
0.15 |
|
x |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
|
y0 |
19.70 |
19.15 |
17.55 |
14.95 |
11.80 |
8.05 |
4.15 |
0.00 |
|
yu |
0.00 |
0.00 |
0.00 |
0.00 |
0.00 |
0.00 |
0.00 |
0.00 |
Согласно рис. 2.11, у0, уuозначают ординаты верхней и нижней стороны профиля относительно оси абсцисс х.
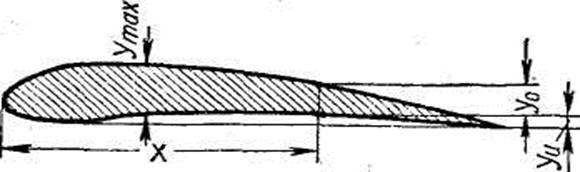
Рис. 2.11 Пояснение условных обозначений.
Соответствующая исходная осевая линия показана на обводах профилей на рис. 2.11. У этих профилей она одновременно совпадает с линией отсчета для угла атаки δ. Кривые на рис. 2.9 называются «полярами», потому что радиус-вектор каждой точки дает коэффициент ζ, нанесенный как результирующая сила крыла; наклон радиуса-вектора этой поляры относительно оси ζа
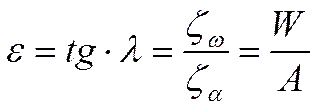
называют «коэффициентом скольжения» (потому что он характеризует угол или наклон траектории полета при планировании крыла). Профиль получается тем лучше, чем меньше этот коэффициент, т. е. чем круче этот радиус-вектор.
Поэтому лучший к. п. д. (лучшее «качество») соответствует точке касания касательной; проведенной из начала координат к поляре. Вследствие малой величины λ имеем:
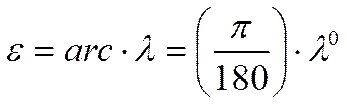
Для профиля, изображенного на рис. 2.9 и 2.10, и упомянутого в табл. 2.1, угол атаки δ дан на рис. 2.10 в зависимости от соответствующего коэффициента подъемной силы ζа. Здесь (на рис. 2.12) точки лучших значений «качества» отмечены кружками. Заслуживает внимания прямолинейность и почти параллельность большинства характеристик.
 |
Рис. 2.12. Коэффициенты подъемной' силы ζа в зависимости от угла атаки для профилей, изображенных на рис. 2.10. Кружками обозначены точки максимального качества.
Следовательно, при проектировании лопрасти ветряного колеса можно использовать для всех или почти для всех сечений один и тот же исходный профиль, причем он утолщается у втулки и делается тоньше к вершине. Нецелесообразно использовать относительную толщину d/Lили ymax/L более 0,20.
Приведенные выше формулы показывают, что небольшая нагрузка на площадь, следовательно низкое значение коэффициента ζa, может быть достигнута с помощью слабой кривизны и небольшой толщины (небольшая нагрузка на площадь может оказаться желательной для водяных насосов в связи с опасностью кавитации, у воздуходувных машин — учитывая близость к звуковой скорости).
При профилировании лопаток играет роль прочность материала,, поскольку одинакового коэффициента ζа можно достигнуть при большей прочности благодаря меньшей толщине стенок ymах или dи тем самым можно получить более удовлетворительные характеристики
Выбор любой формы профиля. Если взять исходным направлением для определения угла атаки направление потока, соответствующее нулевой подъемной силе, и обозначить полученный таким образом угол атаки δ0, то коэффициент подъемной силы для тонкого профиля любой формы при отсутствии трения будет составлять
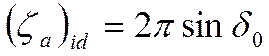
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.